Editorial for Google Code Jam '22 Round 2 Problem D - I, O Bot
Submitting an official solution before solving the problem yourself is a bannable offence.
There is no value in carrying balls across the origin without depositing them into the warehouse, therefore,
collecting the balls with positive coordinates and those with negative coordinates
are two similar but independent tasks. Hence, in what follows, we assume that
for
all
. Moreover, let us assume that the balls are sorted in ascending order by
.
A solution to the problem consists of a number of passes or round-trips from the origin and back
with one or two balls collected in each pass. The time required to collect a single ball
in a pass is
. The time required to collect two balls
and
is
if the balls are of different shapes and
otherwise. We say that two balls
and
are
matched (and write
) if they are
collected in the same pass. Since the order of passes is not affecting the overall time for
collecting all balls, we can equivalently think of the problem as one of finding an optimal
matching of balls.
The following observation will be useful throughout the analysis.
Observation 1: Suppose we want to collect the first balls (
) and
. In an optimal matching, the
-th ball is matched with the
-th ball.
Proof: Consider any matching of balls, where -th ball is not matched with
-th ball, and assume that
-th ball is a
.
- If none of the two balls is matched, we can match the balls and save
seconds.
- If there is a matching
,
, and
-th ball is not matched, then we can match
-th ball with
-th ball instead and save at least
seconds (
, if
-th ball is
-shaped).
- Similarly, if there is a matching
,
, and
-th ball is not matched, we can match
-th ball with
-th ball instead and, again, save at least
seconds.
- Lastly, if there are matchings
and
,
and
, then we can rearrange the matchings as
and
saving at least
seconds.
Test Set 1
Observation 1 helps us match the balls if the last two balls have different shapes. But what if
they have the same shape, say a ?
Observation 2: Suppose we want to collect the first balls (
) and
. There is an optimal matching of balls such that one of the
following conditions holds:
- The last two
-shaped balls
and
are matched.
- There is a matching
with
and, for all
,
. In other words,
-th ball is matched with the nearest
-shaped ball on its left.
- There are no
-shaped balls and
-th ball remains unmatched.
Proof: The full proof is a lengthy case analysis, which we omit here. The idea is
that matching -th ball with the rightmost ball of a particular shape is generally at least
as good as matching with another ball of that shape. For example, suppose that
-th ball
is matched with a
-shaped ball
such that there is another
-shaped ball
with
. If the ball
is unmatched, we can match the ball
with
instead and save
seconds. Otherwise, if the ball
is matched
with some other ball
, we can swap the roles of balls
and
and create
the matchings
and
obtaining the same overall time (if
) or
better.
This means that we can try matching the last -shaped ball with the
-shaped ball before or the rightmost
-shaped ball (if any), and at least one of these moves will be optimal.
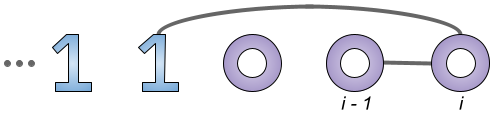
The two observations lead to a dynamic programming solution. Let be the optimum
time to collect the first
-shaped balls and the first
-shaped balls. The base case is
. For
, suppose again that the rightmost of these
balls is
-shaped and it has the coordinate
. The case when the rightmost ball is
-shaped is symmetric.
To eliminate some other corner cases,
,
for
, and
for
. For the general case with
and
, if the penultimate
ball is
-shaped, then
(Observation 1). Otherwise, we can choose to
match the last
-shaped ball with the previous
-shaped ball or the rightmost
-shaped ball (Observation 2),
namely,
.
The final answer is , where
and
denote the total number of
-shaped and
-shaped
balls, respectively. The time complexity of this algorithm is
.
Test Set 2
Using dynamic programming from a different angle, we can solve the problem in linear time, apart from
the initial sorting. Let be the optimum time to collect the first
balls. As
the base cases,
and
. To calculate
for
,
suppose once more that the
-th ball is
-shaped. If the
-th ball is
-shaped, we can
match the last two balls and
(Observation 1). Otherwise, using
Observation 2, we have the options to match the last two
-shaped balls and collect all balls in
seconds, or to match
-th ball with the rightmost
-shaped ball
. The dynamic programming recurrence is not obvious in the latter case, though, as we do
not know the optimum matching for the first
balls except for ball
. What happens
to the
-shaped balls in-between
and
? We are missing another key observation here.
Observation 3: If there is an optimal matching of the first balls such that
the
-shaped ball
is matched with the rightmost
-shaped ball
and
, then
the
-shaped ball
is not matched with another
-shaped ball.
Proof: Assume on the contrary that we have two pairs of matched balls and
,
, such that ball
is
-shaped. These two matched pairs contribute
seconds to the overall matching cost. But then we can rearrange the
matchings as
and
costing us only
seconds, which is
seconds less. This contradicts the optimality assumption of the given matching.
It follows from Observation 3 that the -shaped ball
must be matched with another
-shaped ball,
specifically the rightmost unmatched
-shaped ball. And we can extend this argument and repeatedly
match
-shaped balls with
-shaped balls sweeping leftward for as long as there is another
-shaped ball to
the right of a matched
-shaped ball. This process is illustrated in the drawing below.

Let be the rightmost unmatched ball after the above
-
matching process. There
are no shape changes in the set of balls
and the cost of collecting
those balls is twice the sum
of
-coordinates of
-shaped balls in
. Therefore, the cost of collecting all
balls in this way is
.
can be calculated in
time using prefix sums. But how do we
get the index
efficiently without actually carrying out the matching process? Note that
is the largest index such that
and the set
contains equal number of
-shaped and
-shaped balls. Consider the balance
of
/
balls at
each index
, namely,
, where
and
is the number of
-shaped and
-shaped balls in the set
. The set
has
equal number of
-shaped and
-shaped balls if and only if
. The index
can be looked
up in
time if we maintain a hash-table of indices, when each balance was last
registered. If the current balance
is seen for the first time, it means that there are
not enough
-shaped balls to match all
-shaped balls with, and we can choose
.
We are performing a constant number of operations at each index in this approach, so the overall
time complexity is dominated by the sorting, thus .
Comments