HHPC1 P3 - Yonder Ridge
View as PDFImagine a picturesque landscape made up of various ridges stretching across an -plane. The
-axis of the plane extends from
to
, while the
-axis extends from
to
. There are
ridges numbered from
to
. The
-th ridge can be represented as a line segment connecting
and
, with an aesthetic value of
.
For an interval , the goodness of the landscape from ridge
refers the sum of the aesthetic values of other ridges that are ever strictly above the height of ridge
within
.
A person is planning to explore the landscape, and has a few questions. In the -th question, they wonder what the goodness of landscape
is over the interval
. Note that
is the same for each query.
Constraints
For all subtasks:
Subtask 1 [30%]
Subtask 2 [70%]
No additional constraints.
Input Specification
The first line contains four space-separated integers ,
,
, and
.
The -th of the following
lines each contain three space-separated integers
,
, and
.
The -th of the following
lines each contain two space-separated integers
and
.
Output Specification
For each query, output an integer, representing the goodness of the landscape.
Sample Input
3 15 2 7
6 9 3
2 11 2
10 1 1
1 3
1 4Sample Output
1
3Sample Explanation
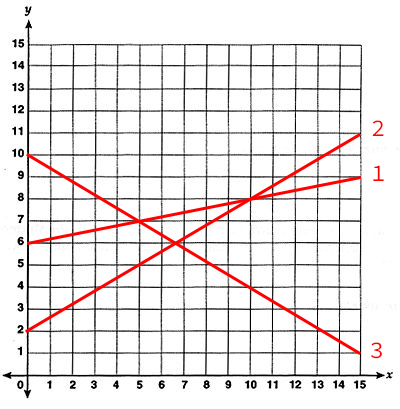
For the first query, only ridge is ever strictly above ridge
in the interval
, so the answer is
.
For the second query, both ridge and ridge
are ever strictly above ridge
at some point in the interval
, so the answer is
.
Comments