ECOO Practice 2014

A recent discovery in the field of astrophysics dealing with the BICEP2 (Background Imaging of Cosmic Extragalactic Polarization) and Keck Array experiments has produced amazing evidence to support the theory of cosmic inflation! Inflation refers to the rapid expansion of the universe at a rate much faster than the speed of light, lasting from ~10^{-36}~ seconds to sometime between ~10^{-33}~ and ~10^{-32}~ seconds after the Big Bang. During this incredibly short period, the volume of the universe was increased by a factor of at least ~10^{78}~. This discovery is a huge step in the direction of confirming the Big Bang theory.

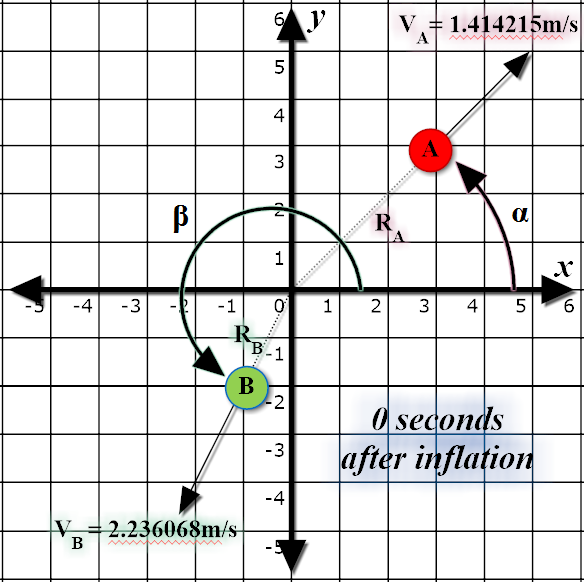
Part of the evidence for the Big Bang theory is the observation that planets and particles in the universe are constantly moving apart from each other. The first particles of the universe (including W and Z bosons and Higgs bosons) formed at the end of the inflationary period and were dispersed throughout the universe. Your task is to model the simple dispersion of two such particles from the singularity at the beginning of the Big Bang.

For simplicity's sake, we will work in 2 dimensions only for this problem. Let us label our particles A and B, and set the "centre" of the universe (where the singularity of the Big Bang is originally concentrated) as the origin of a Cartesian plane, the point ~(0, 0)~. Inflation has already propelled the two particles ~R_A~ and ~R_B~ metres, respectively, away from the centre. The particles, after being accelerated, are now moving at a constant velocity of ~V_A~ and ~V_B \frac m s~ away from the centre. The directions in which particles A and B are moving are, respectively, ~\alpha~ degrees and ~\beta~ degrees counterclockwise relative to the positive ~x~ direction. 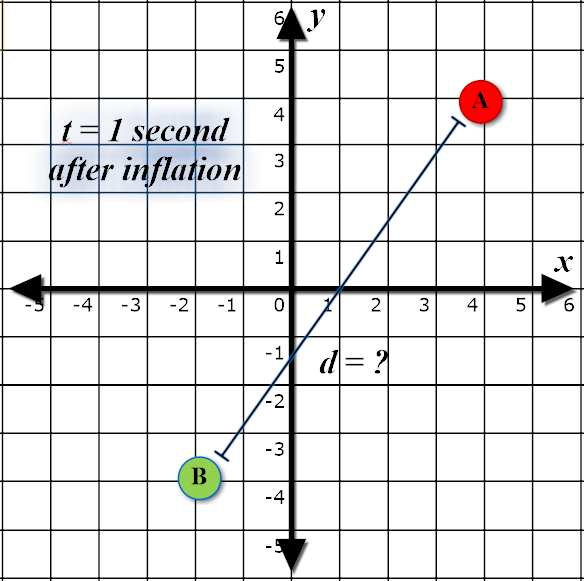Given this information, what is the distance between the particles ~t~ seconds after inflation has ended?

Input Specification

The input will contain 10 test cases. Each test case will consist of a single line with 7 space separated real values, in the order: ~R_A~, ~R_B~, ~V_A~, ~V_B~, ~\alpha~, ~\beta~, and ~t~. It is guaranteed that all values in the input will be less than ~10\,000~ in magnitude, and that the paths of A and B will never overlap.

Output Specification

For each test case, output a single real value, rounded and displayed to exactly 2 decimal places. The distance the particles are from each other after ~t~ seconds has elapsed.

Sample Input (Only 5 examples shown here)

4.242641 2.236068 1.414215 2.236068 45 243.43495 1
100.0 100.0 10.0 10.0 135.0 315.0 100.0
101.99 607.37 16.69 16.54 329.17 317.29 6061.14
162.92 380.26 6.71 5.49 227.61 69.98 3203.42
815.85 681.36 3.61 9.48 207.39 47.93 1540.80

Sample Output

10.00
2200.00
20920.74
38878.86
21378.26

Explanation

The following diagrams depict the first test case in the sample input.