The solution is easiest to up with by considering the 1-dimensional case i.e., a 1-dimensional table (size $N$) with incremental updates and queries on sums of values on an interval. If the values on the table are stored as such, computing the sum of an interval requires $\mathcal{O}(N)$ operations. A query of the sum of values stored on a certain interval $[X,Y]$ can also be answered by computing the cumulative sums $S=[1,X-1]$ and $M=[1,Y]$ and then the answer $A=M-S$. The sums $S$ and $M$ can be stored in the table, in which case the query can be answered in $\mathcal{O}(1)$. Maintaining the sums then causes the update to require $\mathcal{O}(N)$ operations.

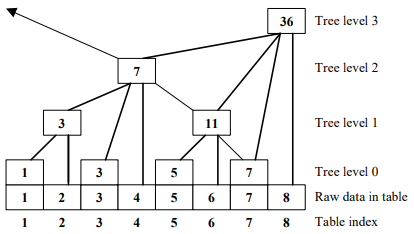
Figure 3. A binary indexed tree with the update structure of the tree in solid lines and a dashed line presenting the path of a query of the sum of the interval $[1,7]$ ($7+11+7=25$). Only the rows marked with the tree level need to be stored.

The binary indexed tree data structure (Figure 3) presented in [1] can support cumulative sum computation and update in $\mathcal{O}(\log N)$ and only takes the same space as the raw table. In the tree the indices run from $1\dots N$ and each cell at index $I$ contains the sum of an interval $[I-2^K+1,I]$ where $K$ is the number of trailing zeroes in the binary representation of the index of the cell. Thus the sum of an interval can be computed with 2 $\mathcal{O}(\log N)$ queries. The next cell in an update can be computed by adding to the current index value its lowest 1 bit. Similarly in a query, the next cell index can be obtained by subtracting the lowest 1-bit. An update requires updating all the cells that contain the sum of an interval containing the cell, this can also be done in $\mathcal{O}(\log N)$ operations. The computation of sums can be made a little faster for small intervals by noting that the cumulative sum queries will eventually hit the same cells and stop at the first common cell (the query ends up adding and subtracting the same cell).

The solution to the 1-dimensional case can be generalized to any number of dimensions (in the case of the IOI competition 2D, i.e., an $N\times N$ table). The trees are placed using the same logic as in the 1-dimensional case forming a tree of trees. In this case, the tree-like structure of the cell at coordinate $(X,Y)$ contains the sum of an area which is determined by the number of zeroes in the binary representation of $X$ in the X-direction and respectively the number of zeroes in the binary representation of $Y$ in the Y-direction. The structure can then support queries of a sum of values in the rectangle $[1,X]\times [1,Y]$ in time $\mathcal{O}({\log }^{2}N)$ (for a $P$-dimensional case $\mathcal{O}({\log }^{P}N)$). The query for a rectangular shape can be expressed in terms of these basic queries (e.g. 4 queries in the 2-dimensional case:

$${\displaystyle sum([L,R]\times [B,T])=sum([1,R]\times [1,T])-sum([1,L-1]\times [1,T])-sum([1,R]\times [1,B-1])+sum([1,L-1]\times [1,B-1]))}$$

(See Figure 4 for examples.) The example solution also optimizes this for small queries using the same method as the 1-dimensional case. The task also requires indexing to start at $0$ and the binary indexed tree data structure requires indexing that starts at $1$.

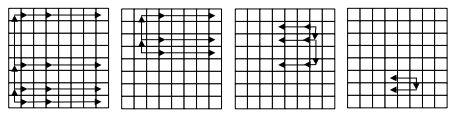
Figure 4. Update and query paths in the 2-dimensional solution from left to right: update $(1,1)$, update $(2,5)$, $sum([1,7]\times [1,7])$, $sum([1,6]\times [1,3])$.

Examples are shown in Figure 5.

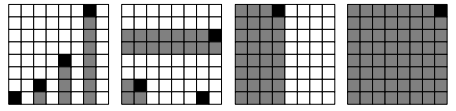
Figure 5. Illustration of some sums of areas stored in different cells, the storing cell is black, the area stored (including the cell) is dark gray.

It is also possible to order the area sums in other ways, in which case the indexing scheme changes.

Reference

[1] P. M. Fenwick, A new data structure for cumulative frequency tables, Software - Practice and Experience 24, 3 (1994), 327-336, 1994