The solution is based on the algorithm, running in ~\mathcal O(n^3)~ time, presented in [1]. Recently, this algorithm is slightly improved in [2], but its implementation is too complicated to accept it for the competition, so we use the algorithm in [1] as a solution.

The diameter of a bus network is the longest length of the route between any two bus stops in the bus network. Our goal is to find the minimum value of the diameters over all possible choices of the hubs and assignments of bus stops. As did in [1], we consider two cases separately. For it, we need some notations. Let ~D_1~ be the minimum value of the longest length between two bus stops which are connected through only one hub over all possible choice of one hub, and let ~D_2~ be the minimum value of the longest length between two bus stops which are connected through both two hubs over all possible choice of two hubs and the corresponding assignments of bus stops. The diameter can be found in the following way presented in [1]. First, compute ~D_1~ and ~D_2~. Next, output the minimum of ~D_1~ and ~D_2~ as the minimum diameter of the entire network.

First we will explain the computation of ~D_1~. If a point ~p~ will be served as the hub through which the longest route passes, the longest length is ~d(p, q) + d(p, r)~, where the points ~q~ and ~r~ is the farthest and the second farthest ones from ~p~, respectively. Then ~D_1 = \min_p\{d(p, q) + d(p, r)\}~ over all points ~p~ of the input. This can be obtained in ~\mathcal O(n^2)~ time because the farthest and second farthest bus stops for each point ~p~ are easily found in ~\mathcal O(n)~ time. Second we will explain how to compute ~D_2~ with a simple example. Note that in this case the longest route between two bus stops will pass both two hubs ~H_1~ and ~H_2~.

We consider all pairs of bus stops of the input as possible two hubs ~H_1~ and ~H_2~, and select the pair of the bus stops that gives a minimum diameter. Let at the beginning ~D_2~ be sufficiently large (e.g., maxint). Consider now fixed two hubs ~H_1~ and ~H_2~. Each of the remaining ~n-2~ points will be initially connected to one of two hubs, say ~H_1~. Sort the remaining ~n-2~ points in the array ~P~ in non-decreasing order according to the distance from the hub ~H_1~ (Figure 1).

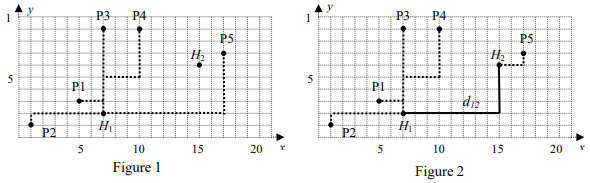
Denote by ~r_1 = d(H_1, P[n-3])~, ~r_2 = d(H_2, P[n-2])~ and ~d_{12} = d(H_1, H_2)~. If ~r_1+d_{12}+r_2 < D_2~, then the point ~P[n-2]~ is connected to the hub ~H_2~ and set ~D_2~ to the new value ~D_2 = r_1+d_{12}+r_2~. Figure 2 represents this step, ~r_1 = d(H_1, P[n-3]) = d(H_1, P[4]) = 10~, ~r_2 = d(H_2, P[n-2]) = (H_2, P[5]) = 3~, ~d_{12} = d(H_1, H_2) = 12~, so ~D_2 = r_1+d_{12}+r_2 = 10+12+3 = 25~. Now we repeat the same procedure with ~r_1 = d(H_1, P[n-4])~, ~r_2 = d(H_2, P[n-3])~, same ~d_{12} = d(H_1, H_2)~, and get ~r_1+d_{12}+r_2 = d(H_1, P[3])+d_{12}+d(H_2, P[4]) = 7+12+8 = 27~. Since we got the new distance which is greater than the previous diameter, the value ~D_2~ remains unchanged, so ~D_2~ still has value ~25~. (If ~25~ is turned out to be the minimum of ~D_2~ at the end of the procedure, the point ~P[4]~ shall be connected to ~H_1~ although its distance to ~H_2~ is smaller than the distance from ~H_1~.) This situation is represented in Figure 3 where the point ~P[4]~ is connected with a thin line to ~H_2~ which is shorter than the distance from ~H_1~ to ~P[4]~.

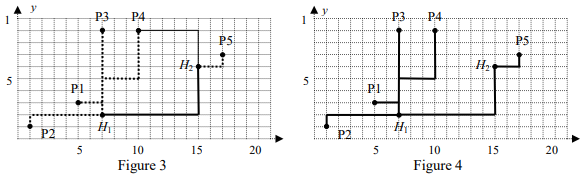
This procedure is repeated by decreasing the index of the array ~P~ one by one until the index ~1~ is reached. For the example, the minimum value of ~D_2~ is ~25~ after the procedure and the corresponding network is shown in Figure 4.

Other approaches

Many contestants may take a (seemingly natural and intuitive) heuristic approach to connect each of ~n-2~ bus stops to the nearest one of two hubs. But this is wrong because there is a counterexample. Of course, this approach can produce correct answers for some inputs.

We can make a brute force algorithm running in ~\mathcal O(n^4)~ time. It considers all pairs of points as hubs ~H_1~ and ~H_2~, and computes ~D(H_1, H_2)~ for each pair in ~\mathcal O(n^2)~ time. But this approach will not produce the answer for large inputs within the time limit.

References

[1] J.-M. Ho, D. T. Lee, C.-H. Chang, C. K Wong, Minimum diameter spanning trees and related problems, SIAM J. on Computing, 20(5):987—997, 1991.

[2] T. Chan, Semi-online maintenance of geometric optima and measures, 13^th ACM-SODA, 474—483, 2002.