A polygon consists of all points on or enclosed by its border.
A convex polygon has the property that for any two points  and
and  of the polygon, the line segment connecting
of the polygon, the line segment connecting  and
and  is inside the polygon.
All polygons in this task are convex polygons with at least two vertices, and all vertices in a polygon are different and have integer coordinates.
No three vertices of a polygon are collinear.
The word "polygon" below always refers to such polygons.
is inside the polygon.
All polygons in this task are convex polygons with at least two vertices, and all vertices in a polygon are different and have integer coordinates.
No three vertices of a polygon are collinear.
The word "polygon" below always refers to such polygons.
Given two polygons  and
and  , the Minkowski sum of
, the Minkowski sum of  and
and  consists of all the points of the form
consists of all the points of the form  where
where  is a point in
is a point in  and
and  is a point in
is a point in  .
It turns out that the Minkowski sum of polygons is also a polygon.
The figure below shows an example: two triangles and their Minkowski sum.
.
It turns out that the Minkowski sum of polygons is also a polygon.
The figure below shows an example: two triangles and their Minkowski sum.
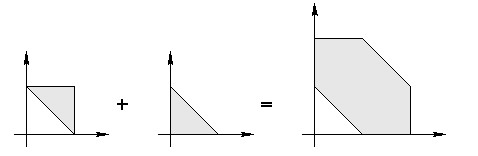
We study a reverse operation to the Minkowski sum. For a given polygon  , we are looking for two polygons
, we are looking for two polygons  and
and  such that:
such that:
 is the Minkowski sum of
is the Minkowski sum of  and
and  ,
, has from
has from  to
to  different vertices, i.e. it is a segment (2 vertices), a triangle (3 vertices) or a quadrilateral (4 vertices),
different vertices, i.e. it is a segment (2 vertices), a triangle (3 vertices) or a quadrilateral (4 vertices), should have as many vertices, as possible, i.e.:
should have as many vertices, as possible, i.e.:
 should be a quadrilateral, if possible,
should be a quadrilateral, if possible,- if
 cannot be a quadrilateral, it should be a triangle, if possible,
cannot be a quadrilateral, it should be a triangle, if possible,
- otherwise it should be a segment.
Clearly, neither  nor
nor  can be equal to
can be equal to  because then the other summand would have to be a point, which is not a valid polygon.
because then the other summand would have to be a point, which is not a valid polygon.
You are given a set of input files, each containing a description of a polygon  .
For each input file you should find the polygons
.
For each input file you should find the polygons  and
and  , as required above, and create an output file containing descriptions of
, as required above, and create an output file containing descriptions of  and
and  .
For the given input files, such polygons
.
For the given input files, such polygons  and
and  can always be found.
If there are many correct results, you should find and output one of them.
can always be found.
If there are many correct results, you should find and output one of them.
Input Specification
The first line contains one integer 
 , the index of the test case.
, the index of the test case.
 indicates that this is a sample test case.
indicates that this is a sample test case.
The second line contains one integer  , the number of vertices of the polygon
, the number of vertices of the polygon  .
.
The following  lines each contain two integers
lines each contain two integers  , the coordinates of the
, the coordinates of the  -th vertex of the polygon.
The vertices are given in counter-clockwise order.
All input coordinates are non-negative integers.
-th vertex of the polygon.
The vertices are given in counter-clockwise order.
All input coordinates are non-negative integers.
Since this is intended to be an output-only problem, when you submit, you can submit a program that only prints the answer based on the test case number in the first line, and run your program locally to get the answer for each test case.
You can view the input files at polygon.zip.
Output Specification
In the first line, output an integer 
 , the number of vertices in polygon
, the number of vertices in polygon  .
.
In the following  lines, output two integers
lines, output two integers 
 , representing the coordinates of a vertex of polygon
, representing the coordinates of a vertex of polygon  .
The vertices should be given in counter-clockwise order.
.
The vertices should be given in counter-clockwise order.
In the next line, output an integer 
 , the number of vertices in polygon
, the number of vertices in polygon  .
.
In the following  lines, output two integers
lines, output two integers 
 , representing the coordinates of a vertex of polygon
, representing the coordinates of a vertex of polygon  .
The vertices should be given in counter-clockwise order.
.
The vertices should be given in counter-clockwise order.
Sample Input
Copy
5
0 1
0 0
2 0
2 1
1 2
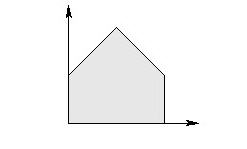
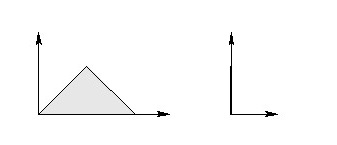
Sample Output 1
Copy
3
0 0
2 0
1 1
2
0 1
0 0
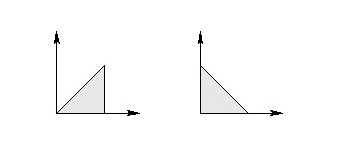
Sample Output 2
Copy
3
0 0
1 0
1 1
3
0 1
0 0
1 0
Explanation for Sample
For the sample input, either of the two outputs above are correct since in both cases  is a triangle and it cannot be a quadrilateral.
is a triangle and it cannot be a quadrilateral.




Comments