Simple solutions

The simplest idea, how to solve this task, can be to implement an algorithm simulating the process of building the flag, following the description given in the task. Such a solution works in ~\mathcal O(n^3)~ time complexity and ~\mathcal O(n^2)~ memory complexity. Clearly, this is not sufficient to receive the full score, but only about ~50\%~. There are also other faster, although not optimal, solutions.

One can employ Breadth First Search (BFS) to reduce the time complexity of the simulation to ~\mathcal O(n^2)~. Initially, we can put into a queue the starting slots (in order of the children's priorities), and then run BFS to simulate the process of building the flag.

Another idea, working in ~\mathcal O(n^2)~ time and ~\mathcal O(1)~ memory, is to just iterate over all the slots, and to determine, whose block will be in each of them. For a given slot, this can be calculated by comparing Manhattan distances¹ to the children's starting points.

There is also an ~\mathcal O(n)~ solution. At first, please observe, that in each row, its leftmost part (possibly empty) is covered by Lucy's blocks, then there may be some Bob's blocks, and finally on the right there may be some Roy's blocks. We can iterate over the rows, and for each of them we can calculate the positions of the boundaries between the mentioned parts. For the first (the bottommost) row, we can do it in ~\mathcal O(n)~ time. Now, having these boundaries for the first row, we can easily compute them for the next row too, because the new left boundary can either be in the same place as the old one or moved to the right. Similarly, the right boundary can move only to the left. This procedure may be continued until Bob's part disappears. The time complexity of this phase is ~\mathcal O(n)~.

When Bob's part disappears, there is only one boundary and we can calculate its position in ~\mathcal O(n)~ time. For all the remaining rows the boundary can either be in the same place as the boundary in the previous row, or can move one place to the right or to the left (depending on the relative vertical positions of Lucy's starting slot, Roy's starting slot and the current row). This phase also takes ~\mathcal O(n)~ time, so the total time complexity of the above algorithm is ~\mathcal O(n)~.

There is another way to obtain an ~\mathcal O(n)~ solution. Given a row, it is possible to calculate the boundaries in ~\mathcal O(1)~ time for this row, independently of the other rows. This can be done by determining in each row the rightmost slot that is not further from Lucy's starting slot than from Bob's starting slot (and similarly such a slot for Bob and Roy, and for Lucy and Roy) — these computations require only simple arithmetic and case decomposition. Using these positions, it is easy to calculate how many slots belong to Lucy, Bob and Roy in each row.

Model solution

The model solution works in ~\mathcal O(1)~ time and memory complexity. It explicitly calculates shapes of the regions covered by Lucy's, Bob's and Roy's blocks. We will show how to determine Bob's region (the other two are calculated analogically). At first, observe, that this region is a figure bounded by the ~X~ axis and some discrete function, let us call it the flag function. Moreover, the domain of this function can be divided into intervals such that, in each interval, the function is either constant or is an arithmetic progression with common difference ~1~ or ~-1~. An example is shown in Figure 1.

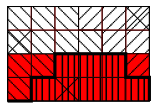
Fig. 1: An example flag function determining the boundary of Bob's region

Now let us imagine, that Roy does not exist. We have only two children, as depicted in Figure 2a. With two children, the flag function always consists of up to three intervals. We can determine them and corresponding function shapes in ~\mathcal O(1)~ time by considering a number of simple cases.

Please note, that this flag function would consist of up to three intervals too, if we had left Bob and Roy only (see Figure 2b).

Having flag functions for Bob and Lucy as well as for Bob and Roy, we can compute the final flag function, which bounds Bob's blocks, as a minimum of these two flag functions. Finally, having this, calculating the appropriate numbers of needed blocks in ~\mathcal O(1)~ time and memory is not very difficult. A similar method can be used to count Lucy's and Roy's blocks.

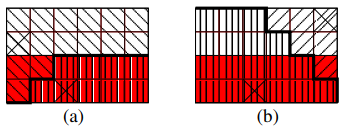
Fig. 2: An example flag function determining the boundary between regions filled with (a) Lucy's and Bob's blocks and (b) Bob's and Roy's blocks

¹ The Manhattan distance between two points is a sum of the absolute differences between their respective coordinates: ~d((x_1,y_1),(x_2,y_2)) = |x_2-x_1|+|y_2-y_1|~.