IOI '07 - Zagreb, Croatia

A new pirate sailing ship is being built. The ship has ~N~ masts (poles) divided into unit sized segments - the height of a mast is equal to the number of its segments. Each mast is fitted with a number of sails and each sail exactly fits into one segment. Sails on one mast can be arbitrarily distributed among different segments, but each segment can be fitted with at most one sail.

Different configurations of sails generate different amounts of thrust when exposed to the wind. Sails in front of other sails at the same height get less wind and contribute less thrust. For each sail we define its inefficiency as the total number of sails that are behind this sail and at the same height. Note that "in front of" and "behind" relate to the orientation of the ship: in the figure below, "in front of" means to the left, and "behind" means to the right.

The total inefficiency of a configuration is the sum of the inefficiencies of all individual sails.

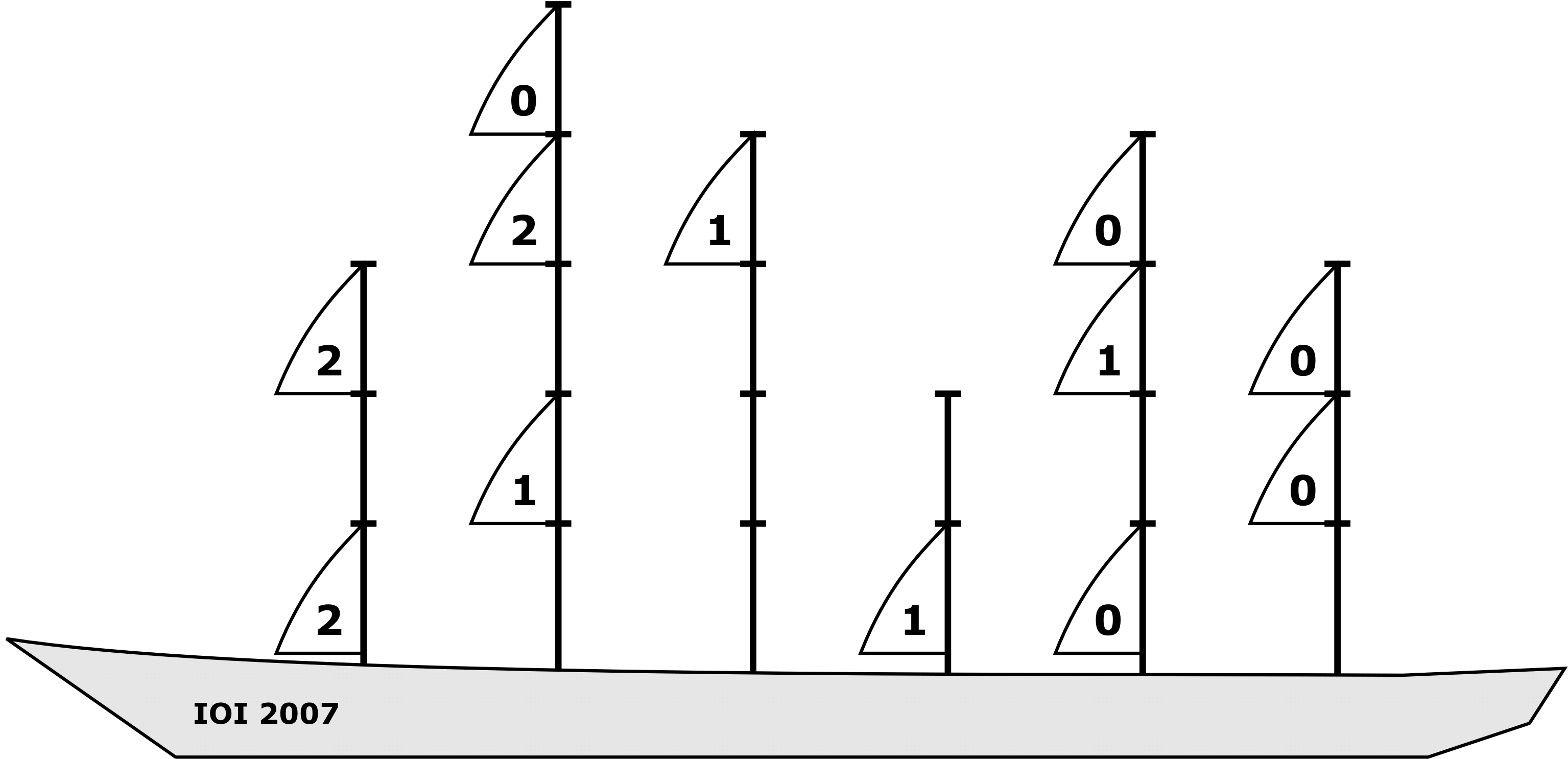frontback
This ship has 6 masts, of heights 3, 5, 4, 2, 4 and 3 from front (left side of image) to back.
This distribution of sails gives a total inefficiency of 10. The individual inefficiency of each sail is written inside the sail.

Write a program that, given the height and the number of sails on each of the ~N~ masts, determines the smallest possible total inefficiency.

Input Specification

The first line of input contains an integer ~N~ ~(2 \le N \le 100\,000)~, the number of masts on the ship. Each of the following ~N~ lines contains two integers ~H~ and ~K~ ~(1 \le H \le 100\,000, 1 \le K \le H)~, the height and the number of sails on the corresponding mast. Masts are given in order from the front to the back of the ship.

Output Specification

Output should consist of a single integer, the smallest possible total inefficiency.

Note: use a 64-bit integer type to calculate and output the result (long long in C/C++, int64 in Pascal).

Sample Input

6
3 2
5 3
4 1
2 1
4 3
3 2

Sample Output

10

Note: In test cases worth a total of 25% of the points, the number of ways to arrange the sails will not exceed ~1\,000\,000~.