Detecting an odd cycle in a graph is a well-known problem. A graph does not contain an odd cycle if and only if it is bipartite. On the other hand, the problem of detecting an even cycle in a graph is not widely known.

We are given a graph consisting of ~N~ vertices and ~M~ edges. Exactly ~N-1~ edges are marked as tree edges and they form a tree. An edge that is not a tree edge will be called a non-tree edge. Every non-tree edge ~e~ has a weight ~w(e)~ associated with it.

The task asks us to find a minimum-weighted set of non-tree edges whose removal results in a graph that does not contain a cycle of even length. We will call such a cycle an even cycle. Reasoning backwards, starting from a graph containing tree edges only, we have to find a maximum-weighted set of non-tree edges that can be added to the graph without forming any even cycles.

In order to describe the model solution, we first need to make a few observations about the structure of the graph we are working with.

Even and odd edges

Consider a non-tree edge ~e=(A, B)~. We define the tree path of the edge ~e~ to be the unique path from ~A~ to ~B~ consisting of tree edges only. If the length of the tree path is even, we say that ~e~ is an even edge; otherwise we say that ~e~ is an odd edge. We will use ~\operatorname{TP}(e)~ to denote the tree path of an edge ~e~.

Obviously, any odd edge present in the graph together with its tree path forms an even cycle. Therefore, we can never include an odd edge in our graph and we can completely ignore them.

Relation between two even edges

Individual even edges may exist in the graph. However, if we include several even edges, an even cycle might be formed. More precisely, if ~e_1~ and ~e_2~ are even edges such that ~\operatorname{TP}(e_1)~ and ~\operatorname{TP}(e_2)~ share a common tree edge, then adding both ~e_1~ and ~e_2~ to the graph necessarily creates an even cycle.

In order to sketch the proof of this claim, consider the two odd cycles created by ~e_1~ and ~e_2~ together with their respective tree paths. If we remove all common tree edges from those cycles we get two paths ~P_1~ and ~P_2~. The parity of ~P_1~ is equal to the parity of the ~P_2~ since we removed the same number of edges from the two initial odd cycles. As ~P_1~ and ~P_2~ also have the same endpoints, we can merge them into one big even cycle.

Tree edges contained in odd cycles

As a direct consequence of the previous claim, we can conclude that every tree edge may be contained in at most one odd cycle.

Conversely, if we add only even edges to the tree in such a way that every tree edge is contained in at most one odd cycle, then we couldn't have formed any even cycles. We briefly sketch the proof of this claim here. If an even cycle existed, it would have to contain one or more non-tree edges. Informally, if it contains exactly one non-tree edge we have a contradiction with the assumption that only even edges are added; if it contains two or more non-tree edges then we will arrive at a contradiction with the second assumption.

Model solution

Now, we can use our observations to develop a dynamic programming solution for the problem. A state is a subtree of the given tree. For each state, we calculate the weight of the maximum-weighted set of even edges that can be added to the subtree while maintaining the property that each tree edge is contained in at most one odd cycle. The solution for the task is the weight associated with the state representing the initial tree.

To obtain a recursive relation, we consider all even edges with tree paths passing through the root of the tree. We can choose to do one of the following:

1. We do not add any even edge whose tree path passes through the root of the tree. In this case, we can delete the root and proceed to calculate the optimal solution for each of the subtrees obtained after deleting the root node.

2. We choose an even edge ~e~ whose tree path passes through the root of the tree and add it to the tree. Next, we delete all tree edges along ~\operatorname{TP}(e)~ (since, now, they are contained in one odd cycle), and, finally, we proceed to calculate the optimal solution for each of the subtrees obtained after deleting the tree path. Add ~w(e)~ to the total sum.

We will use the tree in figure 1 as an example. Figure 2 shows case (1) in the recursive relation (we choose not to include an edge whose tree path passes through the root). Figure 3 shows case (2) in the recursive relation, when we include the even edge ~e=(7, 9)~ in the graph.

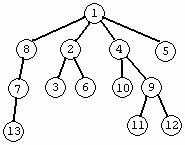
Figure 1

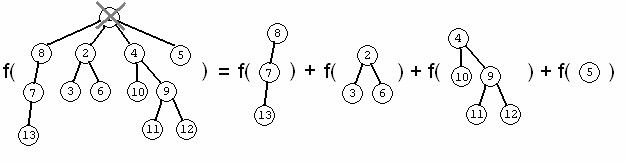
Figure 2

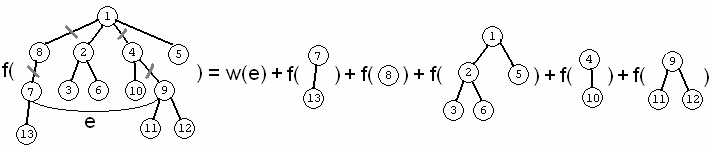
Figure 3

Because of the way the trees are decomposed, all subtrees that appear as subproblems can be represented with an integer and a bitmask. The integer represents the index of the subtree's root node, while the bitmask represents which of the root node's children are removed from the subtree.

The total number of possible states is, therefore, bounded by ~N\cdot 2^K~ where ~K~ is the maximum degree of a node.

Depending on the implementation details, the time complexity of the algorithm can vary. The official implementation has time complexity ~\mathcal O(M \log M + MN + M\cdot 2^K)~.