At any moment during the cutting, we have a set of independent sub-problems — blocks of chocolate. If we find the optimal solution for each of the blocks, together we get the optimal solution for the whole chocolate. This clearly hints at a dynamic programming solution.

Each sub-problem we may encounter corresponds to a rectangular part of the chocolate, and it can be described by four coordinates: specifically, two ~x~ and two ~y~ coordinates — the coordinates of its upper left and lower right corner. Hence we have ~\mathcal O(N^4)~ sub-problems to solve.

Now to solve a given sub-problem, we have to try all possible cuts. There are ~\mathcal O(N)~ possible cuts to try — at most ~N-1~ horizontal and ~N-1~ vertical ones. Each possible cut gives us two new, smaller sub-problems we solve recursively. Obviously, the recursion stops as soon as we reach a ~1 \times 1~ block.

Assume that someone has given us a function ~S(x_1, y_1, x_2, y_2)~ that returns the number of raisins in the rectangle given by coordinates ~(x_1, y_1)~ and ~(x_2, y_2)~ in constant time.

Using this function we can solve the entire problem in ~\mathcal O(N^5)~. We will use recursion with memoization. Given any of the ~\mathcal O(N^4)~ sub-problems, first check the memoization table to see whether we have computed it already. If yes, simply return the previously computed value. Otherwise, proceed as follows: The cost of the first cut is ~S(x_1, y_1, x_2, y_2)~, which we have supposed can be computed in ~\mathcal O(1)~ time. For each possible placement of the first cut, recursively determine the cost of the remaining cuts in each sub-problem, and pick the optimal choice, storing the answer in the memoization table.

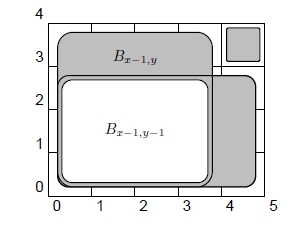
We are only missing one piece of the puzzle: the function ~S~. All possible values can easily be precomputed in ~\mathcal O(N^4)~ and stored in an array.

Alternatively, we can use two-dimensional prefix sums: let ~A~ be the input array, and let ~B_{x,y} = \sum_{i<x} \sum_{j<y} A_{i,j}~. The values ~B~ are called two-dimensional prefix sums. They can be computed using the formula:

$$\displaystyle \forall x, y > 0 : B_{x,y} = B_{x-1,y}+B_{x,y-1}-B_{x-1,y-1}+A_{x-1,y-1}$$

Having the two-dimensional prefix sums, we can compute the sum in any rectangle, using a similar formula. The sum in the rectangle with corners ~(x_1, y_1)~ and ~(x_2, y_2)~ is:

$$\displaystyle S(x_1, y_1, x_2, y_2) = B_{x_2,y_2}-B_{x_1,y_2}-B_{x_2,y_1}+B_{x_1,y_1}$$