Although the employees are already assigned numbers in the input, the numbers can be reassigned in a way that makes them more useful. The supervisor relationships clearly organize the employees into a tree. Assign the new employee numbers in a pre-order walk of the tree3. Figure 1 shows an example of such a numbering.
3 A pre-order walk of a tree first processes the root of that tree, then recursively processes each sub-tree in turn.
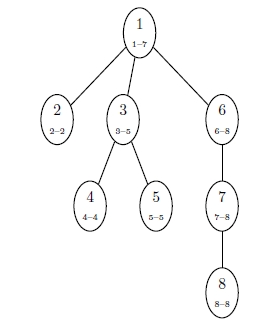
Figure 1: An example of numbering employees by a pre-order walk. The bottom numbers indicate the range of employee numbers in each sub-tree.
A useful property of this numbering is that all the employees in a sub-tree have sequential numbers. For a given employee  , let
, let ![[e]](//static.dmoj.ca/mathoid/873c1b3dc3eafe827f621f6fdc13aa73bc35ac1e/svg) be the range of employee numbers managed by
be the range of employee numbers managed by  . Notice that for a region, we can construct an ordered array of all the interval end-points for that region, and a list of all employees in that region. This can be done during the assignment of numbers in linear time.
. Notice that for a region, we can construct an ordered array of all the interval end-points for that region, and a list of all employees in that region. This can be done during the assignment of numbers in linear time.
Now let us consider how to answer queries  . Let the sizes of the regions be
. Let the sizes of the regions be  and
and  respectively. Given this data structure, a natural solution is to consider every pair of employees
respectively. Given this data structure, a natural solution is to consider every pair of employees  from these regions and check whether
from these regions and check whether  lies in the interval
lies in the interval ![[e_1]](//static.dmoj.ca/mathoid/66aeee277d7e30906ad887cac1a0fa63fb5ff77b/svg) . However, this will take
. However, this will take  time per query, which we can improve upon.
time per query, which we can improve upon.
The interval end-points for region  divide the integers into contiguous blocks. All employees in the same block have the same managers from
divide the integers into contiguous blocks. All employees in the same block have the same managers from  , and we can precompute the number of such managers for each such block. This gives us a faster way to answer queries. Rather than comparing every employee in
, and we can precompute the number of such managers for each such block. This gives us a faster way to answer queries. Rather than comparing every employee in  with every block for
with every block for  , we can observe that both are ordered by employee ID. Thus, one can maintain an index into each list, and in each step advance whichever index is lagging behind the other. Since each index traverses a list once, this takes
, we can observe that both are ordered by employee ID. Thus, one can maintain an index into each list, and in each step advance whichever index is lagging behind the other. Since each index traverses a list once, this takes  time.
time.
Using just this query mechanism can still take  time, because all the queries might involve large regions. However, it is sufficient to earn the points for the tests where no region has more than
time, because all the queries might involve large regions. However, it is sufficient to earn the points for the tests where no region has more than  employees.
employees.
Precomputing queries
In the query algorithm above, it is also possible to replace the list of employees in  with the entire list of employees, and thus compute the answer to all queries for a particular
with the entire list of employees, and thus compute the answer to all queries for a particular  . This still requires only a single pass over the blocks for
. This still requires only a single pass over the blocks for  , so it takes
, so it takes  time to produce all the answers for a particular
time to produce all the answers for a particular  . Similarly, one can iterate over all interval end-points while fixing
. Similarly, one can iterate over all interval end-points while fixing  , giving all answers for a particular
, giving all answers for a particular  .
.
This allows all possible queries to be pre-computed in  time and
time and  memory. This is sufficient to earn the points for the tests where
memory. This is sufficient to earn the points for the tests where  .
.
This algorithm is too slow and uses too much memory to solve all the tests. However, it is not necessary to precompute all answers, just the most expensive ones. We will precompute the answers involving regions with size at least  . There are obviously at most
. There are obviously at most  such regions, so this will take
such regions, so this will take  time and
time and  memory. The remaining queries involve only small regions, so they can be answered in
memory. The remaining queries involve only small regions, so they can be answered in  time. Choosing
time. Choosing  gives
gives  time and
time and  memory, which is sufficient for a full score.
memory, which is sufficient for a full score.
Caching queries
As an alternative to precomputation, one can cache the results of all queries, and take the answer from the cache if the same query is made again. Let  be the number of unique queries. The cost of maintaining the query cache depends on the data structure used; a balanced binary tree gives
be the number of unique queries. The cost of maintaining the query cache depends on the data structure used; a balanced binary tree gives  overhead for this.
overhead for this.
Combining the cache with the  algorithm is sufficient to achieve the points for tests that have either no more than
algorithm is sufficient to achieve the points for tests that have either no more than  employees per region (because this is the case even without the cache), as well as the cases with no more than
employees per region (because this is the case even without the cache), as well as the cases with no more than  regions (since the total cost of all distinct queries together is
regions (since the total cost of all distinct queries together is  ).
).
To achieve a full score with a cache rather than precomputation, one must use a better method for answering queries. Suppose we have a block in  , and wish to find all matching employees from
, and wish to find all matching employees from  . While we have previously relied on a linear walk over the employees from
. While we have previously relied on a linear walk over the employees from  , we can instead use a binary search to find the start and end of the range in
, we can instead use a binary search to find the start and end of the range in  time. This allows the entire query to be answered in
time. This allows the entire query to be answered in  time. A similar transformation (binary searching the blocks for each employee in
time. A similar transformation (binary searching the blocks for each employee in  ) gives
) gives  time for each query.
time for each query.
Now when answering each query, choose the best out of the  ,
,  and
and  query mechanisms. To establish an upper bound on run-time, we will make assumptions about which method is chosen to answer particular types of queries.
query mechanisms. To establish an upper bound on run-time, we will make assumptions about which method is chosen to answer particular types of queries.
Again, divide the problem into large regions with at least  employees and the rest. For queries involving one of the large regions, use the
employees and the rest. For queries involving one of the large regions, use the  algorithm (where
algorithm (where  and
and  are respectively the smaller and larger of
are respectively the smaller and larger of  and
and  ). The caching of queries ensures that this contributes no more than
). The caching of queries ensures that this contributes no more than  time. For the remaining queries, use an
time. For the remaining queries, use an  algorithm. The smaller regions have at most
algorithm. The smaller regions have at most  employees, so this contributes
employees, so this contributes  time.
time.
The optimal value of  occurs when the two parts account for equal time. Solving for this optimal
occurs when the two parts account for equal time. Solving for this optimal  gives a bound of
gives a bound of  for answering non-duplicate queries; combined with the cost for the query cache, this gives an algorithm with time complexity
for answering non-duplicate queries; combined with the cost for the query cache, this gives an algorithm with time complexity  and memory complexity
and memory complexity  .
.
The time bound is marginally worse than for the first solution, but in practical terms this solution runs at about the same speed and uses significantly less memory.

Comments