Pavel has a toy railway. It is very simple. There is a single main line consisting of ~n~ stations. These stations are numbered from ~0~ to ~n-1~ in order along the line. The distance between the stations ~i~ and ~i+1~ is ~l_i~ centimeters (~0 \le i < n-1~).

Apart from the main line there may be some secondary lines. Each secondary line is a railway line between a station on the main line and a new station that does not lie on the main line. (These new stations are not numbered.) At most one secondary line can start in each station of the main line. The length of the secondary line starting at station ~i~ is ~d_i~ centimeters. We use ~d_i = 0~ to denote that there is no secondary line starting at station ~i~.

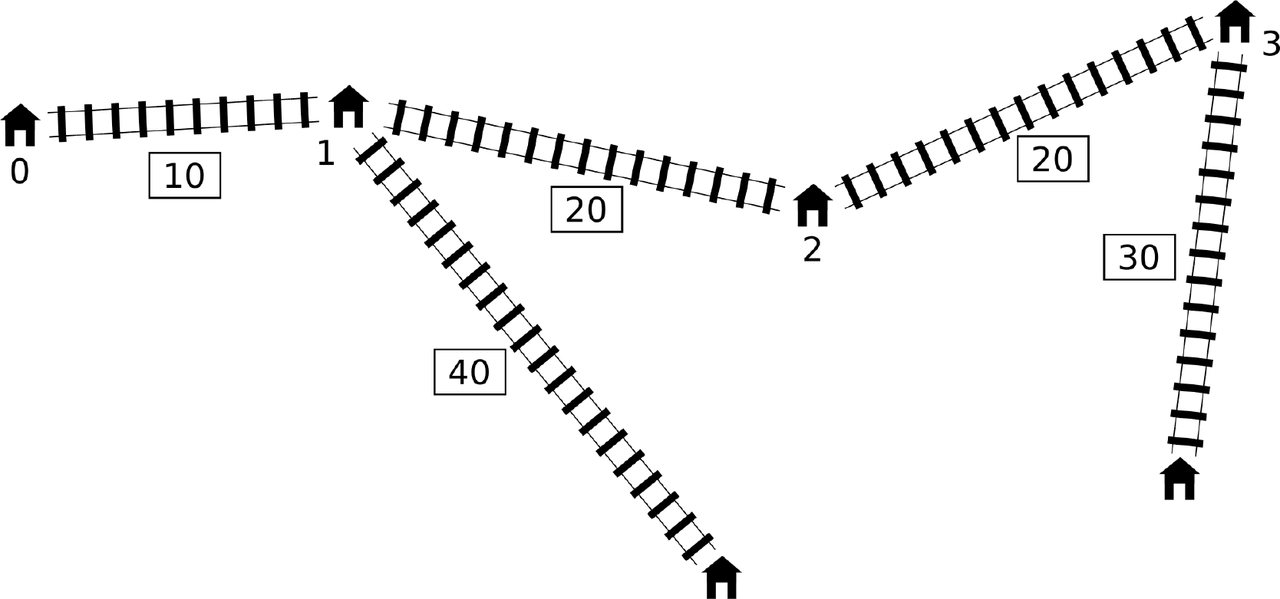
Pavel is now planning to build one shortcut: an express line between two different (possibly neighbouring) stations of the main line. Express line will have length of exactly ~c~ centimeters, regardless of what two stations it will connect.

Each segment of the railway, including the new express line, can be used in both directions. The distance between two stations is the smallest length of a route that goes from one station to the other along the railways. The diameter of the whole railway network is the maximum distance among all pairs of stations. In other words, this is the smallest number ~t~, such that the distance between every pair of stations is at most ~t~.

Pavel wants to build the express line in such a way that the diameter of the resulting network is minimized.

Implementation details

You should implement the function

long long find_shortcut(int n, int l[], int d[], int c)

• n: number of stations on the main line,
• l: distances between stations on the main line (array of length ~n-1~),
• d: lengths of secondary lines (array of length ~n~),
• c: length of the new express line.
• the function should return the smallest possible diameter of the railway network after adding the express line.

Examples

Example 1

For the railway network shown above, the grader would make the following function class:

find_shortcut(4, {10, 20, 20}, {0, 40, 0, 30}, 10)

The optimal solution is the build the express line between stations ~1~ and ~3~, as shown below.

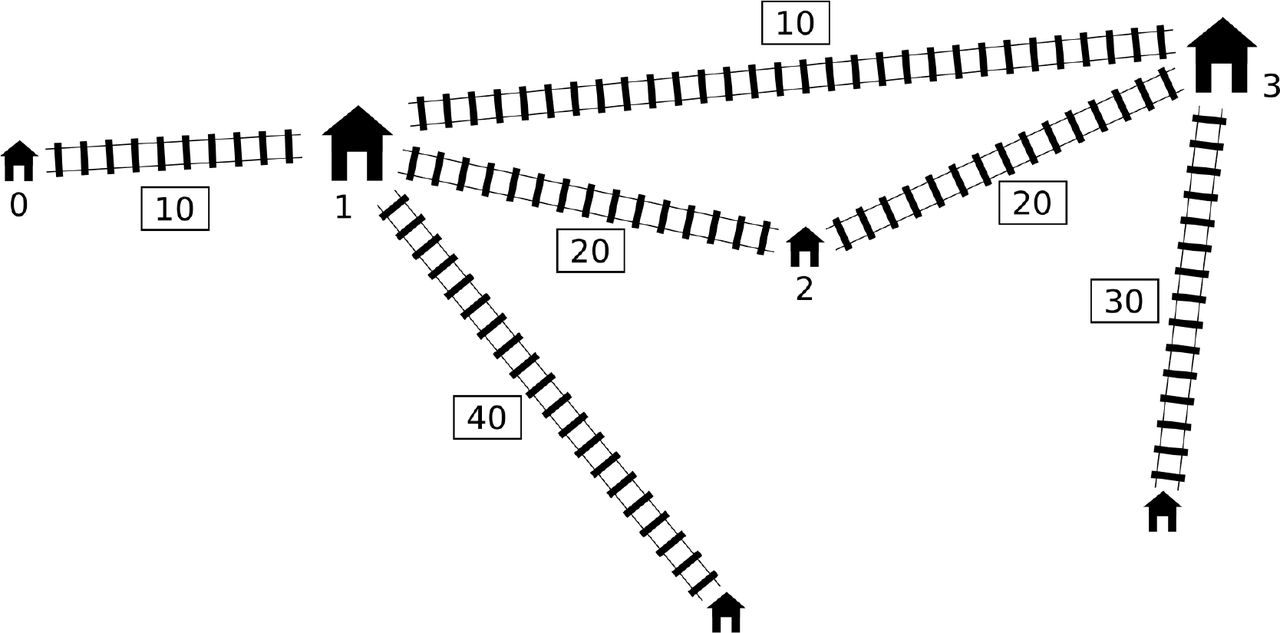
The diameter of the new railway network is ~80~ centimeters, so the function should return ~80~.

Example 2

The grader makes the following function call:

find_shortcut(9, {10, 10, 10, 10, 10, 10, 10, 10}, {20, 0, 30, 0, 0, 40, 0, 40, 0}, 30)

The optimal solution is to connect stations ~2~ and ~7~, in which case the diameter is ~110~.

Example 3

The grader makes the following function call:

find_shortcut(4, {2, 2, 2}, {1, 10, 10, 1}, 1)

The optimal solution is to connect stations ~1~ and ~2~, reducing the diameter to ~21~.

Example 4

The grader makes the following function call:

find_shortcut(3, {1, 1}, {1, 1, 1}, 3)

Connection any two stations with the express line of length ~3~ does not improve the initial diameter of the railway network which is ~4~.

Subtasks

In all subtasks, ~2 \le n \le 1\,000\,000~, ~1 \le l_i \le 10^9~, ~0 \le d_i \le 10^9~, ~1 \le c \le 10^9~.

1. (9 points) ~2 \le n \le 10~
2. (14 points) ~2 \le n \le 100~
3. (8 points) ~2 \le n \le 250~
4. (7 points) ~2 \le n \le 500~
5. (33 points) ~2 \le n \le 3\,000~
6. (22 points) ~2 \le n \le 100\,000~
7. (4 points) ~2 \le n \le 300\,000~
8. (3 points) ~2 \le n \le 1\,000\,000~