IOI '17 P4 - The Big Prize
View as PDFThe Big Prize is a famous TV game show. You are the lucky contestant who has advanced to the final round. You are standing in front of a row of boxes, labeled
through
from left to right. Each box contains a prize that cannot be seen until the box is opened. There are
different types of prizes. The types are numbered from
to
in decreasing order of value.
The prize of type is the most expensive one: a diamond. There is exactly one diamond in the boxes. The prize of type
is the cheapest one: a lollipop. To make the game more exciting, the number of cheaper prizes is much larger than the number of more expensive ones. More specifically, for all
such that
we know the following: if there are
prizes of type
, there are strictly more than
prizes of type
.
Your goal is to win the diamond. At the end of the game, you will have to open a box and you will receive the prize it contains. Before having to choose the box to open you get to ask Rambod, the host of the game show, some questions. For each question, you choose some box . As his answer, Rambod will give you an array
containing two integers. Their meaning is as follows:
- Among the boxes to the left of box
there are exactly
boxes that contain a more expensive prize than the one in box
.
- Among the boxes to the right of box
there are exactly
boxes that contain a more expensive prize than the one in box
.
For instance, suppose that . For your question, you choose the box
. As his response, Rambod tells you that
. The meaning of this response is:
- Exactly one of the boxes
and
contains a prize more expensive than the one in box
.
- Exactly two of the boxes
contain a prize more expensive than the one in box
.
Your task is to find the box containing the diamond by asking a small number of questions.
Implementation details
You should implement the following procedure:
int find_best(int n)
- This procedure is called exactly once by the grader.
: the number of boxes.
- The procedure should return the label of the box which contains the diamond, i.e., the unique integer
such that box
contains a prize of type
.
The above procedure can make calls to the following procedure:
std::vector<int> ask(int i)
: label of the box that you choose to ask about. The value of
must be between
and
, inclusive.
- This procedure returns the array
with
elements. Here,
is the number of more expensive prizes in the boxes to the left of box
and
is the number of more expensive prizes in the boxes to the right of box
.
Example
The grader makes the following procedure call:
find_best(8)
There are boxes. Suppose the prize types are
. All possible calls to the procedure ask and the corresponding return values are listed below.
ask(0)returnsask(1)returnsask(2)returnsask(3)returnsask(4)returnsask(5)returnsask(6)returnsask(7)returns
In this example, the diamond is in box . So the procedure
find_best should return .
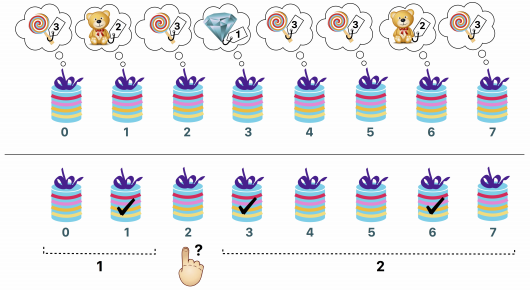
The above figure illustrates this example. The upper part shows the types of the prizes in each box. The lower part illustrates the query ask(2). The marked boxes contain more expensive prizes than the one in box .
Constraints
.
- The type of the prize in each box is between
and
, inclusive.
- There is exactly one prize of type
.
- For all
, if there are
prizes of type
, there are strictly more than
prizes of type
.
Subtasks and scoring
In some test cases, the behavior of the grader is adaptive. This means that in these test cases the grader does not have a fixed sequence of prizes. Instead, the answers given by the grader may depend on the questions asked by your solution. It is guaranteed that the grader answers in such a way that after each answer there is at least one sequence of prizes consistent with all the answers given so far.
- (20 points) There is exactly
diamond and
lollipops (hence,
). You can call the procedure
askat mosttimes.
- (80 points) No additional constraints.
In subtask 2 you can obtain a partial score. Let be the maximum number of calls to the procedure
ask among all test cases in this subtask. Then, your score for this subtask is calculated according to the following table:
| Questions | Score |
|---|---|
Wrong Answer) |
|
Sample grader
The sample grader is not adaptive. Instead, it just reads and uses a fixed array of prize types. For all
, the type of the prize in box
is given as
. The sample grader expects input in the following format:
- line
:
- line
:
The sample grader prints a single line containing the return value of find_best and the number of calls to the procedure ask.
Sample graders are provided for you below:
Or if you prefer, prize.zip with all 3 files.
You can compile the files yourself by adding them to your IDE or by using the command gcc grader.c prize.c or g++ grader.c prize.c
Comments
The partial score is not working :( . I should have gotten 90 points not 100
Edit: All hail the Dark Lord Quantum and his Ancient Magicks.
Partial scoring works now. All submissions have been rejudged.
Just curious, but is the grader on the judge adaptive?
This comment is hidden due to too much negative feedback. Show it anyway.
But that statement was from the official contest. I was wondering whether this is still the case here.