According to ancient Persian legends in Shahnameh, Zal, the legendary Persian hero, is madly in love with Rudaba, the princess of Kabul. When Zal asked for Rudaba's hand in marriage, her father gave him a challenge.

In Persia there are cities, labeled from ~0~ to ~n-1~, and ~m~ two-way roads, labeled from ~0~ to ~m-1~. Each road connects a pair of distinct cities. Each pair of cities is connected by at most one road. Some of the roads are royal roads used for travels by royals. Zal's task is to determine which of the roads are the royal roads.

Zal has a map with all the cities and the roads in Persia. He does not know which of the roads are royal, but he can get help from Simurgh, the benevolent mythical bird who is Zal's protector. However, Simurgh does not want to reveal the set of royal roads directly. Instead, she tells Zal that the set of all royal roads is a golden set. A set of roads is a golden set if and only if:

• it has exactly ~n-1~ roads, and
• for every pair of cities, it is possible to reach one from the other by traveling only along the roads of this set.

Furthermore, Zal can ask Simurgh some questions. For each question:

1. Zal chooses a golden set of roads, and then
2. Simurgh tells Zal how many of the roads in the chosen golden set are royal roads.

Your program should help Zal find the set of royal roads by asking Simurgh at most ~q~ questions. The grader will play the role of Simurgh.

Implementation details

You should implement the following procedure:

std::vector<int> find_roads(int n, std::vector<int> u, std::vector<int> v)

• ~n~: number of cities,
• ~u~ and ~v~: arrays of length ~m~. For all ~0 \le i \le m-1~, ~u[i]~ and ~v[i]~ are the cities connected by road ~i~.
• This procedure should return an array of length ~n-1~ containing the labels of the royal roads (in an arbitrary order).

Your solution can make at most ~q~ calls to the following grader procedure:

int count_common_roads(const std::vector<int>& r)

• ~r~: array of length ~n-1~ containing the labels of roads in a golden set (in an arbitrary order).
• This procedure returns the number of royal roads in ~r~.

Example

find_roads(4, [0, 0, 0, 1, 1, 2], [1, 2, 3, 2, 3, 3])

find_roads(...)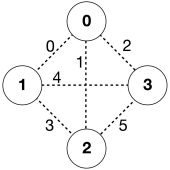

count_common_roads([0, 1, 2]) = 2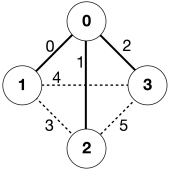

count_common_roads([5, 1, 0]) = 3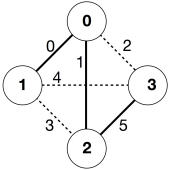

In this example there are ~4~ cities and ~6~ roads. We denote by ~(a,b)~ a road connecting cities ~a~ and ~b~. The roads are labeled from ~0~ to ~5~ in the following order: ~(0,1)~, ~(0,2)~, ~(0,3)~, ~(1,2)~, ~(1,3)~, and ~(2,3)~. Every golden set has ~n-1 = 3~ roads.

Assume that the royal roads are the roads labeled ~0~, ~1~, and ~5~, that is, the roads ~(0,1)~, ~(0,2)~, and ~(2,3)~. Then:

• count_common_roads([0, 1, 2]) returns ~2~. This query is about roads labeled ~0~, ~1~, and ~2~, that is, roads ~(0,1)~, ~(0,2)~, and ~(0,3)~. Two of them are royal roads.
• count_common_roads([5, 1, 0]) returns ~3~. This query is about the set of all royal roads.

The procedure find_roads should return ~[5, 1, 0]~ or any other array of length ~3~ that contains these three elements.

Note that the following calls are not allowed:

• count_common_roads([0, 1]): here the length of ~r~ is not ~3~.
• count_common_roads([0, 1, 3]): here ~r~ does not describe a golden set, because it is impossible to travel from city ~0~ to ~3~ only using the roads ~(0,1)~, ~(0,2)~, ~(1,2)~.

Constraints

• ~2 \le n \le 500~
• ~n-1 \le m \le n(n-1)/2~
• ~0 \le u[i], v[i] \le n-1~ (for all ~0 \le i \le m-1~)
• For all ~0 \le i \le m-1~, road ~i~ connects two different cities (i.e., ~u[i] \ne v[i]~).
• There is at most one road between each pair of cities.
• It is possible to travel between any pair of cities through the roads.
• The set of all royal roads is a golden set.
• find_roads should call count_common_roads at most ~q~ times. In each call, the set of roads specified by ~r~ should be a golden set.

Subtasks

1. (13 points) ~n \le 7~, ~q = 30\,000~
2. (17 points) ~n \le 50~, ~q = 30\,000~
3. (21 points) ~n \le 240~, ~q = 30\,000~
4. (19 points) ~q = 12\,000~ and there is a road between every pair of cities
5. (30 points) ~q = 8000~

Sample grader

The sample grader reads the input in the following format:

• line ~1~: ~n\ m~
• line ~2+i~ (for all ~0 \le i \le m-1~): ~u[i]\ v[i]~
• line ~2+m~: ~s[0]\ s[1]\ \dots\ s[n-2]~

Here, ~s[0]\ s[1]\ \dots\ s[n-2]~ are the labels of the royal roads.

The sample grader outputs YES, if find_roads calls count_common_roads at most ~30\,000~ times, and returns the correct set of royal roads. Otherwise, it outputs NO.

Beware that the procedure count_common_roads in the sample grader does not check whether ~r~ has all properties of a golden set. Instead, it counts and returns the number of labels of royal roads in the array ~r~. However, if the program you submit calls count_common_roads with a set of labels that does not describe a golden set, the grading verdict will be Wrong Answer.

Technical note

The procedure count_common_roads in C++ and Pascal uses the pass by reference method for efficiency reasons. You can still call the procedure in the usual way. The grader is guaranteed not to change the value of ~r~.