Aunty Khong is organising a competition with $x$ participants, and wants to give each participant a bag of biscuits. There are $k$ different types of biscuits, numbered from $0$ to $k-1$. Each biscuit of type $i$ $(0\le i\le k-1)$ has a tastiness value of $2^i$. Aunty Khong has $a[i]$ (possibly zero) biscuits of type $i$ in her pantry.

Each of Aunty Khong's bags will contain zero or more biscuits of each type. The total number of biscuits of type $i$ in all the bags must not exceed $a[i]$. The sum of tastiness values of all biscuits in a bag is called the total tastiness of the bag.

Help Aunty Khong find out how many different values of $y$ exist, such that it is possible to pack $x$ bags of biscuits, each having total tastiness equal to $y$.

Implementation details

You should implement the following procedure:

long long count_tastiness(long long x, std::vector<long long> a)

• $x$: the number of bags of biscuits to pack.
• $a$: an array of length $k$. For $0\le i\le k-1$, $a[i]$ denotes the number of biscuits of type $i$ in the pantry.
• The procedure should return the number of different values of $y$, such that Aunty can pack $x$ bags of biscuits, each one having a total tastiness of $y$.
• The procedure is called a total of $q$ times (see Constraints and Subtasks sections for the allowed values of $q$). Each of these calls should be treated as a separate scenario.

Examples

Example 1

Consider the following call:

count_tastiness(3, {5, 2, 1})

This means that Aunty wants to pack $3$ bags, and there are $3$ types of biscuits in the pantry:

• $5$ biscuits of type $0$, each having a tastiness value $1$,
• $2$ biscuits of type $1$, each having a tastiness value $2$,
• $1$ biscuit of type $2$, having a tastiness value $4$.

The possible values of $y$ are $[0,1,2,3,4]$. For instance, in order to pack 3 bags of total tastiness $3$, Aunty can pack:

• one bag containing three biscuits of type $0$, and
• two bags, each containing one biscuit of type $0$ and one biscuit of type $1$.

Since there are $5$ possible values of $y$, the procedure should return $5$.

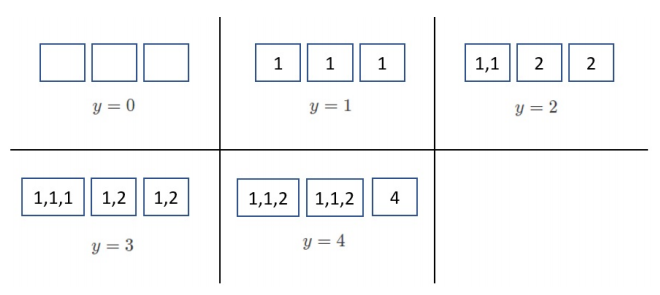
Example 2

Consider the following call:

count_tastiness(2, {2, 1, 2})

This means that Aunty wants to pack $2$ bags, and there are $3$ types of biscuits in the pantry:

• $2$ biscuits of type $0$, each having a tastiness value $1$,
• $1$ biscuit of type $1$, having a tastiness value $2$,
• $2$ biscuits of type $2$, each having a tastiness value $4$.

The possible values of $y$ are $[0,1,2,4,5,6]$. Since there are $6$ possible values of $y$, the procedure should return $6$.

Constraints

• $1\le k\le 60$
• $1\le q\le 1000$
• $1\le x\le {10}^{18}$
• $0\le a[i]\le {10}^{18}$ (for all $0\le i\le k-1$)
• For each call to count_tastiness, the sum of tastiness values of all biscuits in the pantry does not exceed ${10}^{18}$.

Subtasks

1. ($9$ points) $q\le 10$, and for each call to count_tastiness, the sum of tastiness values of all biscuits in the pantry does not exceed $100000$.
2. ($12$ points) $x=1,q\le 10$
3. ($21$ points) $x\le 10000,q\le 10$
4. ($35$ points) The correct return value of each call to count_tastiness does not exceed $200000$.
5. ($23$ points) No additional constraints.

Sample grader

The sample grader reads the input in the following format. The first line contains an integer $q$. After that, $q$ pairs of lines follow, and each pair describes a single scenario in the following format:

• line $1$: $k$ $x$
• line $2$: $a[0]$ $a[1]$ $\dots$ $a[k-1]$

The output of the sample grader is in the following format:

• line $i$ $(1\le i\le q)$: return value of count_tastiness for the $i$-th scenario in the input.