IOI '21 P5 - Dungeons Game
View as PDFRobert is designing a new computer game. The game involves one hero, opponents and
dungeons. The opponents are numbered from
to
and the dungeons are numbered from
to
. Opponent
is located in dungeon
and has strength
. There is no opponent in dungeon
.
The hero starts off entering dungeon , with strength
. Every time the hero enters any dungeon
, they confront opponent
, and one of the following occurs:
- If the hero's strength is greater than or equal to the opponent's strength
, the hero wins. This causes the hero's strength to increase by
. In this case the hero enters dungeon
next
.
- Otherwise, the hero loses. This causes the hero's strength to increase by
. In this case the hero enters dungeon
next.
Note may be less than, equal to, or greater than
. Also,
may be less than, equal to, or greater than
. Regardless of the outcome of the confrontation, the opponent remains in dungeon
and maintains strength
.
The game ends when the hero enters dungeon . One can show that the game ends after a finite number of confrontations, regardless of the hero's starting dungeon and strength.
Robert asked you to test his game by running simulations. For each simulation, Robert defines a starting dungeon
and starting strength
. Your task is to find out, for each simulation, the hero's strength when the game ends.
Implementation Details
You should implement the following procedures:
void init(int n, std::vector<int> s, std::vector<int> p, std::vector<int> w, std::vector<int> l)
: number of opponents.
,
,
,
: arrays of length
. For
:
is the strength of the opponent
. It is also the strength gained by the hero after winning against opponent
.
is the strength gained by the hero after losing against opponent
.
is the dungeon the hero enters after winning against opponent
.
is the dungeon the hero enters after losing against opponent
.
- This procedure is called exactly once, before any calls to
simulate(see below).
long long simulate(int x, int z)
: the dungeon the hero enters first.
: the hero's starting strength.
- This procedure should return the hero's strength when the game ends, assuming the hero starts the game by entering dungeon
, having strength
.
- The procedure is called exactly
times.
Examples
Consider the following call:
init(3, {2, 6, 9}, {3, 1, 2}, {2, 2, 3}, {1, 0, 1})
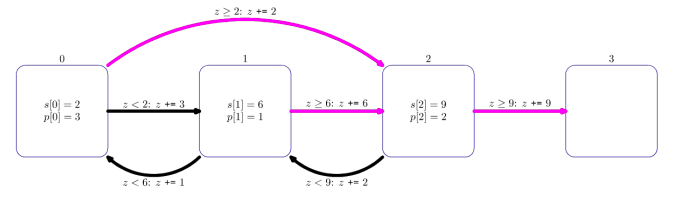
The diagram above illustrates this call. Each square shows a dungeon. For dungeons ,
and
, the values
and
are indicated inside the squares. Magenta arrows indicate where the hero moves after winning a confrontation, while black arrows indicate where the hero moves after losing.
Let's say the grader calls simulate(0, 1).
The game proceeds as follows:
| Dungeon | Hero's strength before confrontation | Result |
|---|---|---|
| Lose | ||
| Lose | ||
| Win | ||
| Lose | ||
| Win | ||
| Win | ||
| Game ends |
As such, the procedure should return .
Let's say the grader calls simulate(2, 3).
The game proceeds as follows:
| Dungeon | Hero's strength before confrontation | Result |
|---|---|---|
| Lose | ||
| Lose | ||
| Win | ||
| Lose | ||
| Win | ||
| Win | ||
| Game ends |
As such, the procedure should return .
Constraints
(for all
)
(for all
)
(for all
)
Subtasks
- (
points)
(for all
)
- (
points)
(for all
)
- (
points)
, all opponents have the same strength, in other words,
for all
.
- (
points)
, there are at most
distinct values among all values of
.
- (
points)
- (
points) No additional constraints.
Sample Grader
The sample grader reads the input in the following format:
- line
:
- line
:
- line
:
- line
:
- line
:
- line
:
for the
-th call to
simulate.
The sample grader prints your answers in the following format:
- line
: the return value of the
-th call to
simulate.
Attachment Package
The sample grader and sample test cases are available here: dungeons.zip.
Comments
edit: sorry it seems that it can't be 2GB for system reasons :(
ML should be 2GB.