IOI '22 P4 - Digital Circuit
View as PDFThere is a circuit, which consists of gates numbered from
to
.
Gates
to
are threshold gates, whereas gates
to
are source gates.
Each gate, except for gate , is an input to exactly one threshold gate.
Specifically, for each
such that
, gate
is an input to gate
, where
.
Importantly, we also have
.
Moreover, we assume
.
Each threshold gate has one or more inputs.
Source gates do not have any inputs.
Each gate has a state which is either or
.
The initial states of the source gates are given by an array
of
integers.
That is, for each
such that
, the initial state of the source gate
is
.
The state of each threshold gate depends on the states of its inputs and is determined as follows.
First, each threshold gate is assigned a threshold parameter.
The parameter assigned to a threshold gate with inputs must be an integer between
and
(inclusive).
Then, the state of a threshold gate with parameter
is
, if at least
of its inputs have state
, and
otherwise.
For example, suppose there are threshold gates and
source gates.
The inputs to gate
are gates
and
, the inputs to gate
are gates
,
, and
, and the only input to gate
is gate
.
This example is illustrated in the following picture.
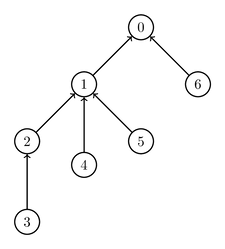
Suppose that source gates and
have state
, while source gates
and
have state
.
Assume we assign parameters
,
and
to threshold gates
,
and
respectively.
In this case, gate
has state
, gate
has state
and gate
has state
.
This assignment of parameter values and the states is illustrated in the following picture.
Gates whose state is
are marked in black.
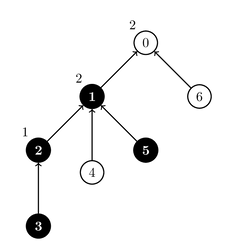
The states of the source gates will undergo updates.
Each update is described by two integers
and
and toggles the states of all source gates numbered between
and
, inclusive.
That is, for each
such that
, source gate
changes its state to
, if its state is
, or to
, if its state is
.
The new state of each toggled gate remains unchanged until it is possibly toggled by one of the later updates.
Your goal is to count, after each update, how many different assignments of parameters to threshold gates result in gate having state
.
Two assignments are considered different if there exists at least one threshold gate that has a different value of its parameter in both assignments.
As the number of ways can be large, you should compute it modulo
.
Note that in the example above, there are different assignments of parameters to threshold gates, since gates
,
and
have
,
and
inputs respectively.
In
out of these
assignments, gate
has state
.
Implementation Details
Your task is to implement two procedures.
void init(int N, int M, std::vector<int> P, std::vector<int> A)
: the number of threshold gates.
: the number of source gates.
: an array of length
describing the inputs to the threshold gates.
: an array of length
describing the initial states of the source gates.
- This procedure is called exactly once, before any calls to
count_ways.
int count_ways(int L, int R)
,
: the boundaries of the range of source gates, whose states are toggled.
- This procedure should first perform the specified update, and then return the number of ways, modulo
, of assigning parameters to the threshold gates, which result in gate
having state
.
- This procedure is called exactly
times.
Example
Consider the following sequence of calls:
init(3, 4, {-1, 0, 1, 2, 1, 1, 0}, {1, 0, 1, 0})
This example is illustrated in the task description above.
count_ways(3, 4)
This toggles the states of gates and
, i.e. the state of gate
becomes
, and the state of gate
becomes
.
Two ways of assigning the parameters which result in gate
having state
are illustrated in the pictures below.
| Way |
Way |
|---|---|
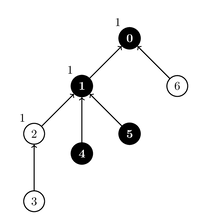 |
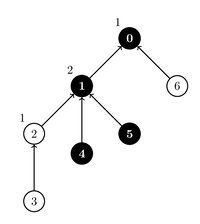 |
In all other assignments of parameters, gate has state
.
Thus, the procedure should return
.
count_ways(4, 5)
This toggles the states of gates and
.
As a result, all source gates have state
, and for any assignment of parameters, gate
has state
.
Thus, the procedure should return
.
count_ways(3, 6)
This changes the states of all source gates to .
As a result, for any assignment of parameters, gate
has state
.
Thus, the procedure should return
.
Constraints
and
(for each
such that
)
- Each threshold gate has at least one input (for each
such that
there exists an index
such that
and
).
(for each
such that
)
Subtasks
- (2 points)
,
,
- (7 points)
,
, each threshold gate has exactly two inputs.
- (9 points)
,
- (4 points)
,
(for some positive integer
),
(for each
such that
),
- (12 points)
,
(for some positive integer
),
(for each
such that
)
- (27 points) Each threshold gate has exactly two inputs.
- (28 points)
- (11 points) No additional constraints.
Sample Grader
The sample grader reads the input in the following format:
- line
:
- line
:
- line
:
- line
:
for update
The sample grader prints your answers in the following format:
- line
: the return value of
count_waysfor update
Attachment Package
The sample grader along with sample test cases are available here.
Comments