IOI '23 P1 - Closing Time
View as PDFHungary is a country with cities, numbered from
to
.
The cities are connected by bidirectional roads, numbered from
to
. For each
such
that
, road
connects city
and city
and has length
, that is, it allows
one to travel between the cities in
units of time. Each road connects two different cities, and
each pair of cities is connected by at most one road.
A path between two distinct cities and
is a sequence
of distinct cities, such that:
,
,
- for each
, there is a road connecting cities
and
.
It is possible to travel from any city to any other city by using the roads, that is, there exists a path between every two distinct cities. It can be shown that this path is unique for each pair of distinct cities.
The length of a path is the sum of the lengths of the t roads connecting consecutive
cities along the path.
In Hungary, many people travel to attend the Foundation Day festivities in two major cities. Once
the celebrations are over, they return to their homes. The government wants to prevent the crowd
from disturbing the locals, so they plan to lock down all cities at certain times. Each city will be
assigned a non-negative closing time by the government. The government has decided that the
sum of all closing times must not be more than . More precisely, for every
between
and
, inclusive, the closing time assigned to city
is a nonnegative integer
. The sum of all
must
not be greater than
.
Consider a city and some assignment of closing times. We say that a city
is reachable from city
if and only if either
, or the path
between these two cities (so in particular
and
) satisfies the following conditions:
- the length of the path
is at most
, and
- the length of the path
is at most
, and
- the length of the path
is at most
.
This year, the two main festival sites are located in city and city
. For each assignment of
closing times, the convenience score is defined as the sum of the following two numbers:
- The number of cities reachable from city
.
- The number of cities reachable from city
.
Note that if a city is reachable from city and reachable from city
, it counts twice towards the
convenience score.
Your task is to compute the maximum convenience score that can be achieved by some assignment of closing times.
Implementation Details
You should implement the following procedure.
int max_score(int N, int X, int Y, long long K, std::vector<int> U, std::vector<int> V, std::vector<int> W)
: the number of cities.
: the cities with main festival sites.
: the upper bound on the sum of closing times.
: arrays of length
describing road connections.
: array of length
describing road lengths.
- This procedure should return the maximum convenience score that can be achieved by some assignment of closing times.
- This procedure may be called multiple times in each test case.
Example
Consider the following call:
max_score(7, 0, 2, 10,
[0, 0, 1, 2, 2, 5], [1, 3, 2, 4, 5, 6], [2, 3, 4, 2, 5, 3])
This corresponds to the following road network:
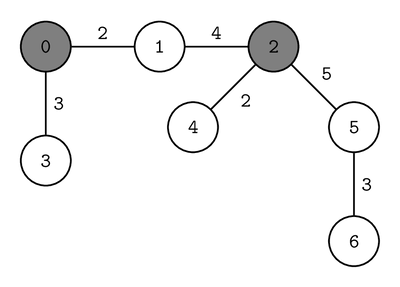
Suppose the closing times are assigned as follows:
| City | |||||||
|---|---|---|---|---|---|---|---|
| Closing time |
Note that the sum of all closing times is , which is not more than
. Cities
,
, and
are
reachable from city
, while cities
,
, and
are reachable from city
.
Therefore, the convenience score is 3 + 3 = 6. There is no assignment of closing times with
convenience score more than 6, so the procedure should return 6.
Also, consider the following call:
max_score(4, 0, 3, 20, [0, 1, 2], [1, 2, 3], [18, 1, 19])
This corresponds to the following road network:
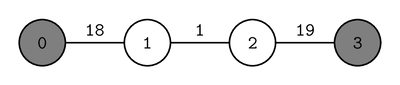
Suppose the closing times are assigned as follows:
| City | ||||
|---|---|---|---|---|
| Closing time |
City is reachable from city
, while cities
and
are reachable from city
.
Therefore, the convenience score is
. There is no assignment of closing times with
convenience score more than
, so the procedure should return
.
Constraints
(for each
such that
)
(for each
such that
)
- It is possible to travel from any city to any other city by using the roads.
, where
is the sum of
over all calls to
max_scorein each test case.
Subtasks
We say that a road network is linear if road connects cities
and
(for each
such that
).
- (
points) The length of the path from city
to city
is greater than
.
- (
points)
, the road network is linear.
- (
points)
, the road network is linear.
- (
points)
, the road network is linear.
- (
points)
- (
points)
- (
points)
- (
points)
- (
points) No additional constraints.
Sample Grader
Let denote the number of scenarios, that is, the number of calls to
max_score. The sample
grader reads the input in the following format:
- line
:
The descriptions of scenarios follow.
The sample grader reads the description of each scenario in the following format:
- line
:
- line
:
The sample grader prints a single line for each scenario, in the following format:
- line
: the return value of
max_score
Attachment Package
The sample grader along with sample test cases are available here.
Comments