IOI '23 P4 - Beech Tree
View as PDFVétyem Woods is a famous woodland with lots of colorful trees. One of the oldest and tallest beech trees is called Ős Vezér.
The tree Ős Vezér can be modeled as a set of nodes and
edges. Nodes are numbered
from
to
and edges are numbered from
to
. Each edge connects two distinct nodes
of the tree. Specifically, edge
connects node
to node
, where
.
Node
is called the parent of node
, and node
is called a child of node
.
Each edge has a color. There are possible edge colors numbered from
to
. The color of
edge
is
. Different edges may have the same color.
Note that in the definitions above, the case does not correspond to an edge of the tree. For
convenience, we let
and
.
For example, suppose that Ős Vezér has nodes and
possible edge colors, with
edges described by connections
and colors
. The tree is displayed in the following figure:
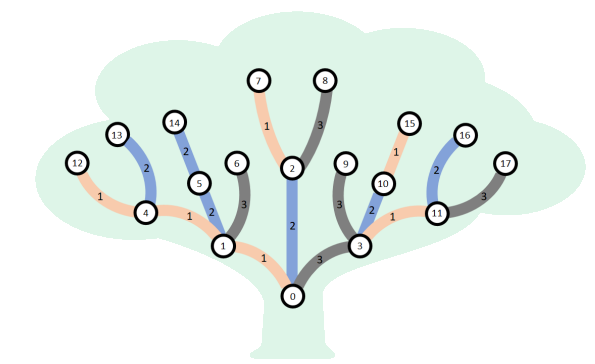
Árpád is a talented forester who likes to study specific parts of the tree called subtrees. For each
such that
, the subtree of node
is the set
of nodes with the following properties:
- Node
belongs to
.
- Whenever a node
belongs to
, all children of
also belong to
.
- No other nodes belong to
.
The size of the set is denoted as
.
Árpád recently discovered a complicated but interesting subtree property. Árpád's discovery involved a lot of playing with pen and paper, and he suspects you might need to do the same to understand it. He will also show you multiple examples you can then analyze in detail.
Suppose we have a fixed and a permutation
of the nodes in the subtree
.
For each such that
, let
be the number of times the color
appears in the
following sequence of
colors:
.
(Note that is always
because the sequence of colors in its definition is empty.)
The permutation is a beautiful permutation if and only if all the following
properties hold:
.
- For each
such that
, the parent of node
is node
.
For any such that
, the subtree
is a beautiful subtree if and only if there exists a
beautiful permutation of the nodes in
. Note that according to the definition every subtree
which consists of a single node is beautiful.
Consider the example tree above. It can be shown that the subtrees and
of this tree are
not beautiful. The subtree
is beautiful, as it consists of a single node. Below, we will show
that the subtree
is also beautiful.
Consider the sequence of distinct integers . This
sequence is a permutation of the nodes in
. The figure below depicts this permutation. The
labels attached to the nodes are the indices at which those nodes appear in the permutation.
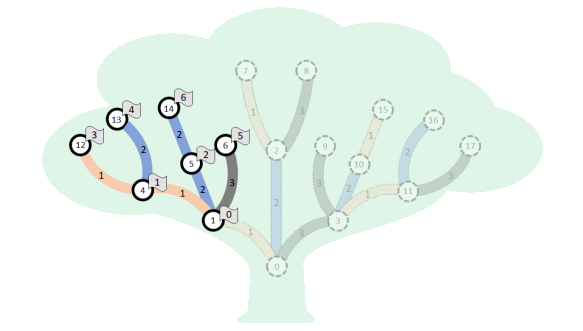
We will now verify that this is a beautiful permutation.
.
since
appears
times in the sequence
.
- Correspondingly, the parent of
. That is, the parent of node
is node
. (Formally,
.)
- Correspondingly, the parent of
since
appears
times in the sequence
.
- Correspondingly, the parent of
. That is, the parent of
is
.
- Correspondingly, the parent of
since
appears
time in the sequence
.
- Correspondingly, the parent of
is
. That is, the parent of
is
.
- Correspondingly, the parent of
since
appears
time in the sequence
.
- Correspondingly, the parent of
is
. That is, the parent of
is
.
- Correspondingly, the parent of
since
appears
times in the sequence
.
- Correspondingly, the parent of
is
. That is, the parent of
is
.
- Correspondingly, the parent of
since
appears
times in the sequence
.
- Correspondingly, the parent of
is
. That is, the parent of
is
.
- Correspondingly, the parent of
As we could find a beautiful permutation of the nodes in , the subtree
is a beautiful subtree.
Your task is to help Árpád decide for every subtree of Ős Vezér whether it is beautiful.
Implementation Details
You should implement the following procedure.
std::vector<int> beechtree(int N, int M, std::vector<int> P, std::vector<int> C)
: the number of nodes in the tree.
: the number of possible edge colors.
: arrays of length N describing the edges of the tree.
- This procedure should return an array
of length
. For each
such that
,
should be
if
is beautiful, and
otherwise.
- This procedure is called exactly once for each test case.
Examples
Example 1
Consider the following call:
beechtree(4, 2, [-1, 0, 0, 0], [0, 1, 1, 2])The tree is displayed in the following figure:
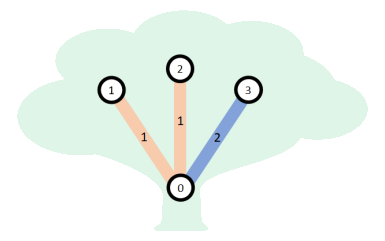
,
, and
each consist of a single node and are therefore beautiful.
is not
beautiful. Therefore, the procedure should return
.
Example 2
Consider the following call:
beechtree(18, 3, [-1, 0, 0, 0, 1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 10, 11, 11], [0, 1, 2, 3, 1, 2, 3, 1, 3, 3, 2, 1, 1, 2, 2, 1, 2, 3])This example is illustrated in the task description above.
The procedure should return .
Example 3
Consider the following call:
beechtree(7, 2, [-1, 0, 1, 1, 0, 4, 5], [0, 1, 1, 2, 2, 1, 1])This example is illustrated in the following figure.
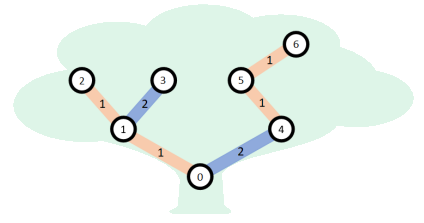
is the only subtree that is not beautiful. The procedure should return
.
Constraints
(for each
such that
)
(for each
such that
)
and
Subtasks
- (9 points)
and
- (5 points) Edge
connects node
to node
. That is, for each
such that
,
.
- (9 points) Each node other than node
is either connected to node
, or is connected to a node which is connected to node
. That is, for each
such that
, either
or
.
- (8 points) For each
such that
, there are at most two edges of color
.
- (14 points)
and
- (14 points)
and
- (12 points)
- (17 points)
- (12 points) No additional constraints.
Sample Grader
The sample grader reads the input in the following format:
- line
:
- line
:
- line
:
Let denote the elements of the array returned by beechtree. The sample grader
prints your answer in a single line, in the following format:
- line
:
Attachment Package
The sample grader along with sample test cases are available here.
Comments