IOI '95 P2 - Shopping Offers
View as PDFIOI '95 - Eindhoven, Netherlands
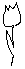 =
2,
=
2,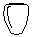 =
5,
=
5,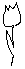 +
+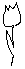 +
+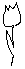 =
5,
=
5,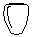 +
+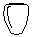 +
+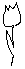 =
10,
=
10, +
+ +
+ +
+ +
+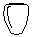 = ?
= ?In a shop each kind of product has a price. For example, the price of a
flower is ICU (Informatics Currency Units) and the price of a vase is
ICU. In order to attract more customers, the shop introduces some
special offers.
A special offer consists of one or more product items for a reduced price. Examples:
- three flowers for
ICU instead of
, or
- two vases together with one flower for
ICU instead of
.
Write a program that calculates the price a customer has to pay for certain items, making optimal use of the special offers. That is, the price should be as low as possible. You are not allowed to add items, even if that would lower the price.
For the prices and offers given above, the (lowest) price for three
flowers and two vases is ICU: two vases and one flower for the
reduced price of
ICU and two flowers for the regular price of
ICU.
Input Specification
The input has a set of offers followed by a purchase.
| Line |
|
| Line |
Each line describes an offer using several integers. The first integer is |
| Line |
The first line contains the number |
| Line |
Each of the subsequent |
Output Specification
A single line with one integer: the lowest possible price to be paid for the purchases.
Sample Input
2
1 7 3 5
2 7 1 8 2 10
2
7 3 2
8 2 5Sample Output
14
Comments