Bitaro will participate in an aerobatics competition. In this competition, Bitaro will fly an airplane. The airplane will keep a certain altitude, and pass through the checkpoints. The area where the airplane will fly is considered as a coordinate plane. There are ~N~ checkpoints, numbered from ~1~ to ~N~. The coordinate of the checkpoint ~i~ (~1 \le i \le N~) is ~(X_i, Y_i)~.

During the competition, the airplane must pass through each checkpoint once. More precisely, the airplane must fly in the following way.

1. First, Bitaro chooses the starting checkpoint, and the airplane will start flying from there.
2. Repeat the following ~N-1~ times: Among the checkpoints which are not yet chosen, Bitaro chooses a checkpoint as the next checkpoint. Then the airplane will fly straight from the current checkpoint to the next checkpoint.
3. When the airplane arrived at the last checkpoint, the flight is finished.

Here, in step 2, we consider the starting checkpoint as an already chosen checkpoint. The airplane must fly straight from a checkpoint to the next checkpoint. It is forbidden to draw a curve or make a turn on the way.

The route of the airplane is a polygonal line. During the flight, the airplane will change its direction at most ~N-2~ times. If the angle of the polygonal line at a checkpoint is small, the change of the direction of the airplane at that checkpoint is large, and there is a risk of failure of the flight.

Therefore, Bitaro wants to make the minimum angle of the polygonal line at the ~N-2~ checkpoints, except for the starting checkpoint and the last checkpoint, as large as possible.

Given the coordinates of the checkpoints, find an order of the checkpoints to pass so that the minimum angle of the polygonal line is as large as possible.

Input Specification

The input data is given in the following format. Given values are all integers. Here, ~Z_0~ is a parameter used by the grader.

~N~ ~Z_0~
~X_1~ ~Y_1~
~\vdots~
~X_N~ ~Y_N~

Output Specification

The output should consist of ~N~ lines. The ~k~-th line (~1 \le k \le N~) of the output should contain the integer ~P_k~ (~1 \le P_k \le N~), which is the ~k~-th checkpoint in the route of the airplane. Here, the starting checkpoint is the first checkpoint ~P_1~.

Constraints

• ~3 \le N \le 1\,000~.
• ~\sqrt{X_i^2+Y_i^2} \le 10\,000\,000~ (~1 \le i \le N~).
• ~(X_i, Y_i) \ne (X_j, Y_j)~ (~1 \le i < j \le N~).
• ~1 \le Z_0 \le 179~.

Library

In this task, you can use a library which contains a function calculating an angle determined by three points. The library is contained in the file aerobatics.h in the archive. The specification is as follows.

• double GetAngle(int xa, int ya, int xb, int yb, int xc, int yc)
  This function calculates the angle ~BAC~ in degrees. It returns a real number with sufficiently small error. Make sure the order of the parameters.
  • Concerning the point ~A~, the parameter xa is the ~x~-coordinate of the point ~A~, and the parameter ya is the ~y~-coordinate of the point ~A~.
  • Concerning the point ~B~, the parameter xb is the ~x~-coordinate of the point ~B~, and the parameter yb is the ~y~-coordinate of the point ~B~.
  • Concerning the point ~C~, the parameter xc is the ~x~-coordinate of the point ~C~, and the parameter yc is the ~y~-coordinate of the point ~C~.
  • If the coordinates of the points ~A~, ~B~ are the same or the coordinates of the points ~A~, ~C~ are the same, the behavior of this function is undefined.

In your program calculating the solutions of this task, you may use the function GetAngle in the library. If you use it, you may modify the function.

The GetAngle is the same as the function used by the grader.

Grading

For each output data, your score is calculated in the following way.

If your output is incorrect, your score is ~0~. For example, if the output sequence ~P_1, P_2, \dots, P_N~ is not a permutation of ~1, 2, \dots, N~ or the format of the output is incorrect, your score is ~0~.

If your output is correct, your score is calculated as follows. Let ~Z~ (degree) be the minimum angle of the polygonal line at the ~N-2~ checkpoints, except for the starting checkpoint and the last checkpoint. Then your score ~S~ is calculated by the following formula.

• If ~Z \ge Z_0~, your score is ~S~.
• If ~Z < Z_0~, your score is ~S \times \frac{f(Z/180)}{f(Z_0/180)}~.

Here the function ~f(\alpha)~ (~0 \le \alpha \le 1~) is defined by ~f(\alpha) = 4\alpha^4 + \alpha~.

Your score for this task is the sum of your scores for the ~6~ input data, rounded to the nearest integer.

For each input data, the values of ~N~, ~Z_0~ and the score are given in the following table:

Subtask	Input Data	~N~	~Z_0~	score
~1~	input_01.txt	~15~	~100~	~10~
~2~	input_02.txt	~200~	~143~	~15~
~3~	input_03.txt	~200~	~134~	~15~
~4~	input_04.txt	~1\,000~	~156~	~20~
~5~	input_05.txt	~1\,000~	~150~	~20~
~6~	input_06.txt	~1\,000~	~153~	~20~

Sample Input

7 90
3 1
2 5
0 2
-1 6
-3 1
-1 -4
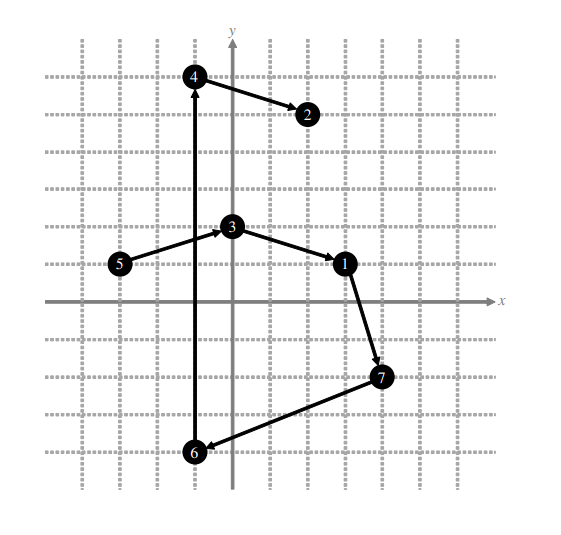
4 -2

Sample Output

5
3
1
7
6
4
2

Explanation for Sample

If the airplane will pass through the checkpoints ~5, 3, 1, 7, 6, 4, 2~ in this order, the route of the airplane is as in the following figure. The checkpoint with the smallest angle is checkpoint ~6~. Its angle is ~68.19859\dots~ (degree). Since ~Z_0 = 90~ (degree), your score for this output will be about ~61.5\%~ of the score of this input data.

Attachment Package

The test cases and the helper library are available here.