JOI '23 Open P2 - Cell Automaton
View as PDFWe have a sufficiently large
There is a cell, which is the origin of the coordinates. Let
At time
- If a cell is black at time
- If a cell is gray at time
- A cell which is white at time
Write a program which, given the information of the colors of the cells at time
Input Specification
Read the following data from the standard input.
Output Specification
Write
Input Constraints
- Given values are all integers.
Subtasks
- (4 points)
- (12 points)
- (8 points)
- (8 points)
- (17 points)
- (25 points)
- (26 points) No additional constraints.
Sample Input 1
2 3
0 2
1 0
0
1
2Sample Output 1
2
8
12Explanation for Sample 1
The following figure shows the colors of the cells at time
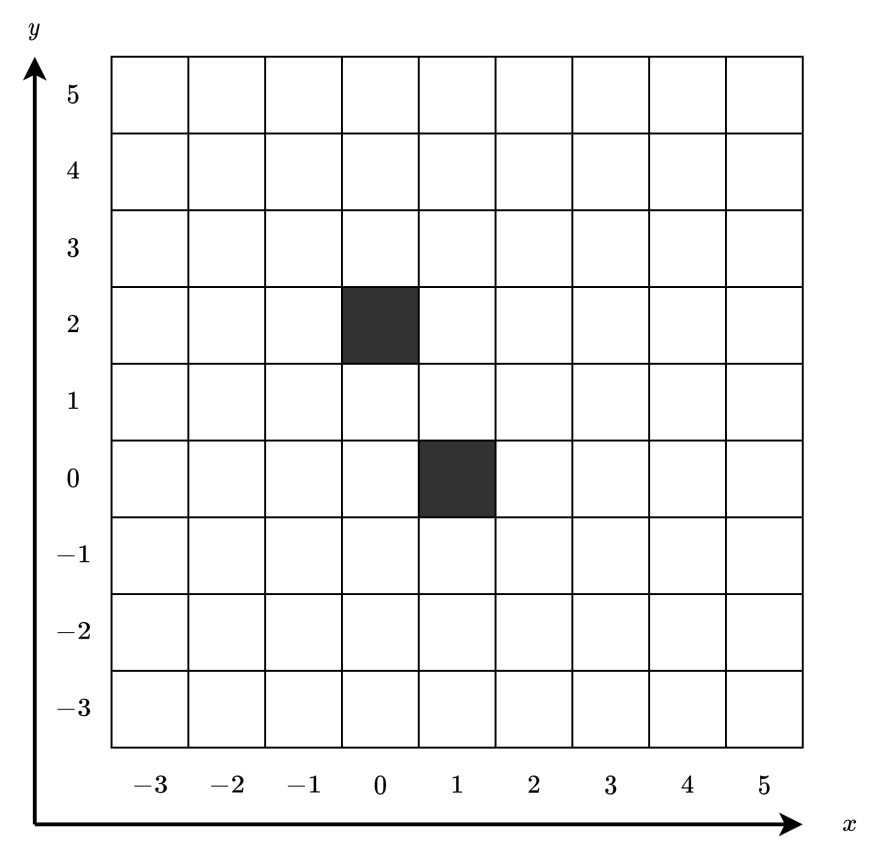
The following figure shows the colors of the cells at time
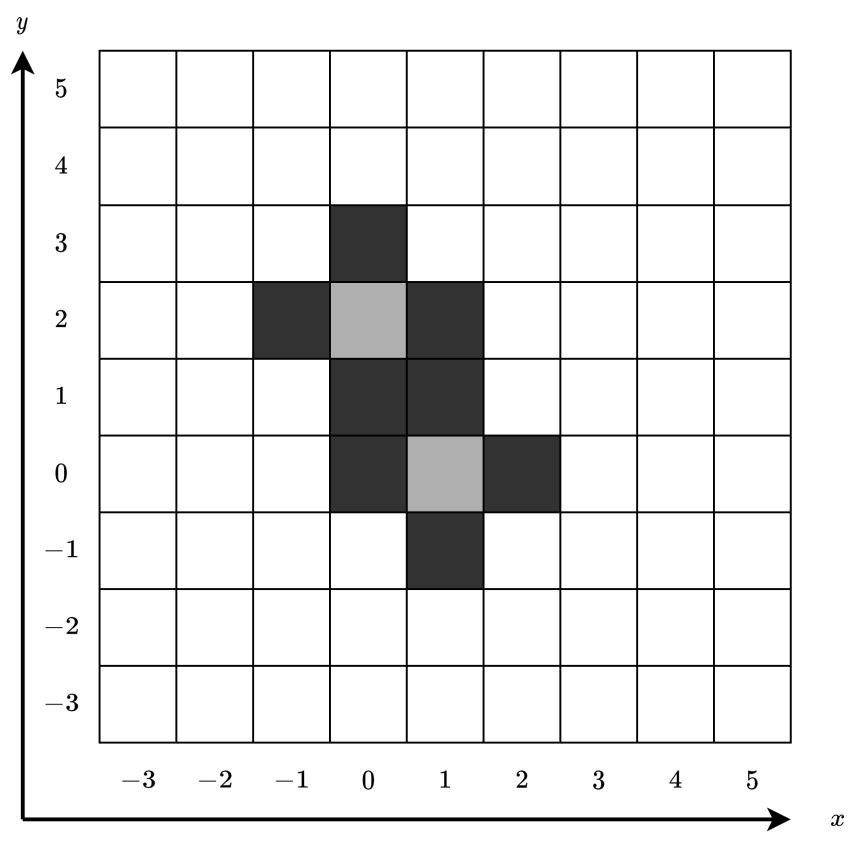
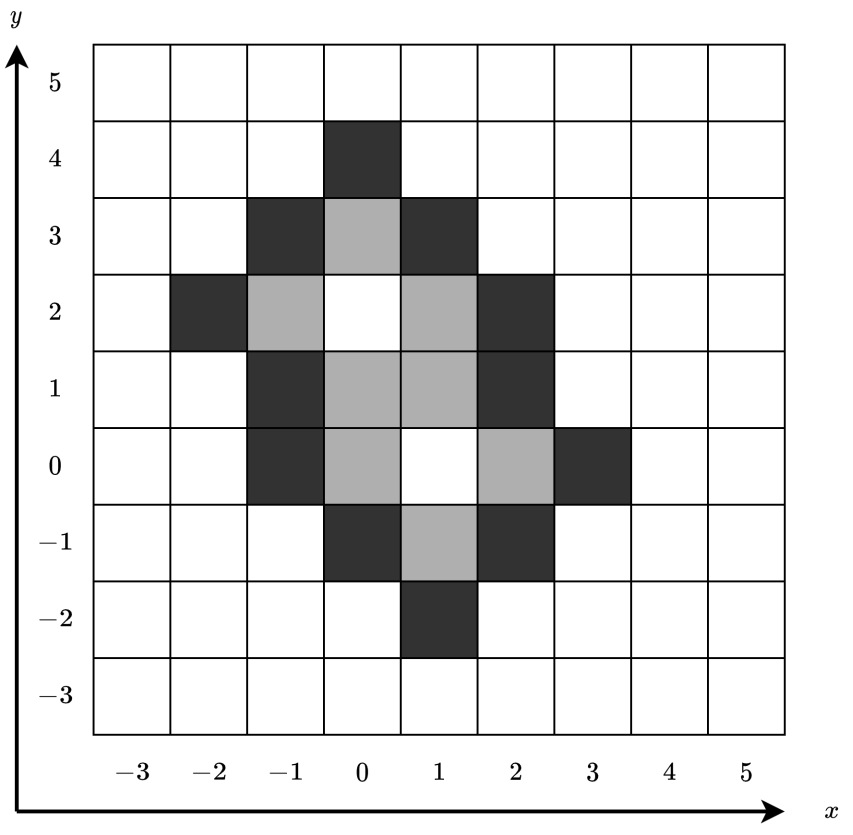
The following figure shows the colors of the cells at time
This sample input satisfies the constraints of Subtasks
Sample Input 2
3 5
0 0
2 2
5 5
0
1
2
3
4Sample Output 2
3
12
21
24
26Explanation for Sample 2
This sample input satisfies the constraints of Subtasks
Sample Input 3
4 10
-3 -3
3 3
-4 4
4 -4
0
1
2
3
4
5
6
7
8
9Sample Output 3
4
16
32
48
56
56
55
56
60
64Explanation for Sample 3
This sample input satisfies the constraints of Subtasks
Comments