Editorial for MALD Contest 1 P5 - Scratch Cat and Desktop Backgrounds

Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.

Author: Lost

Hint 1

How can you find the difference in ones and zeroes in $\mathcal O(1)$ ?

Hint 2

Using a difference array where 1 $= 1$ and 0 $= -1$ , how can you rearrange the $I(S)$ formula? How can you deal with the absolute value?

Subtask 1

This problem is solvable in $\mathcal O(|T|^2)$ by iterating all substrings of $T$ . For each $r$ position (end position of substring), decrement all $l$ positions (start position of substring) and keep track of ones and zeroes. Alternatively, you can iterate all unique pairs of $l$ and $r$ and use a prefix sum array. Increment your answer if the current substring $S$ has an $I(S)$ value between $b_l$ and $b_r$ . Using a $64$ -bit floating point (double) won't pass due to precision errors.

Complexity: $\mathcal O(|T|^2)$

Full Solution

Update a difference array where 1 $= 1$ and 0 $= -1$ . After accumulation, $\text{psa}[r] - \text{psa}[l-1]$ now represents $f_1 - f_0$ in the range $[l, r]$ .

Step 1. Finding fₗ(K) : Substrings With Imbalance ≤ K (Without Absolute Value>

Let $f_l(x)$ (less) denote the number of substrings with $I(S)$ (without absolute value) $\le x$ .

The imbalance $I(S)$ of the substring $S$ from $l$ to $r$ is $\frac{|\text{psa}[r]-\text{psa}[l-1]|}{r-(l-1)} \times 100$ . To make the equation easier to deal with, we will remove the absolute value for now.

We can algebraically manipulate the inequality: $\displaystyle \frac{\text{psa}[r]-\text{psa}[l-1]}{r-(l-1)} \times 100 \le K$ $\displaystyle 100 \times \text{psa}[r] - 100 \times \text{psa}[l-1] \le Kr - K(l-1)$ $\displaystyle 100 \times \text{psa}[r] - Kr \le 100 \times \text{psa}[l-1] - K(l-1)$ For each $r$ value (iterate left to right), count the number of $l$ positions with a greater or equal $100 \times \text{psa}[x] - Kx$ value. Inversion counting can be done in $\mathcal O(\log N)$ using a BIT (Fenwick Tree) or an order statistics tree.

Modifying a tree from the GNU PBDS library allows it to behave like a multiset with order statistic operations. Using a tree from the GNU PBDS library in C++ is much shorter to type but is about ten times slower than a BIT. Subtask $3$ compensates those who typed the longer and faster BIT solution.

Step 2. Finding fₛₗ(x) : Substrings With Imbalance < K (Without Absolute Value>

Let $f_{sl}(x)$ (strictly less) denote the number of substrings with $I(S)$ (without absolute value) $< x$ .

We can algebraically manipulate the same inequality from step $1$ but with $<$ instead of $\le$ . This results in $100 \times \text{psa}[r] - Kr < 100 \times \text{psa}[l-1] - K(l-1)$ .

You should now find $100 \times \text{psa}[x] - Kx$ values strictly greater instead of greater than or equal. You will need to tweak your BIT or ordered statistics tree to accommodate this. When using a BIT, $100 \times \text{psa}[x] - Kx$ values can reach values like $100 \times -10^6 - 100 \times 10^6 = -2 \times 10^8$ . What you can do is compress $100 \times \text{psa}[x] - Kx$ values so they fit. Some large constant factor compression implementations might not pass subtask $3$ .

Step 3. Finding Substrings With Imbalance < K and ≤ K (With Absolute Value)

Remember that $f_l(x)$ and $f_{sl}(x)$ are calculated using the $I(S)$ formula without the absolute value. Because $\text{psa}[r] - \text{psa}[l-1]$ can be negative (more zeroes than ones), you need to count the substrings between $-K$ and $K$ .

Recall $f_l(x)$ (less) is our answer from step $1$ : the number of substrings with $I(S)$ (without absolute value) $\le x$ .

Recall $f_{sl}(x)$ (strictly less) is our answer from step $2$ : the number of substrings with $I(S)$ (without absolute value) $< x$ .

We can modify them to work for absolute values:

For the number of substrings $S$ ~S~ with $I(S) \le K$ ~I(S) \le K~ (with absolute value), we should be finding the number of $I(S)$ ~I(S)~ in the range $[-K, K]$ ~[-K, K]~:

$S$

$I(S)$

$[-K, K] = f_l(K) - f_{sl}(-K)$

For the number of substrings $S$ ~S~ with $I(S) < K$ ~I(S) < K~ (with absolute value), we should be finding the number of $I(S)$ ~I(S)~ in the range $(-K, K)$ ~(-K, K)~:

$S$

$I(S)$

$(-K, K) = f_{sl}(K) - f_l(-K)$

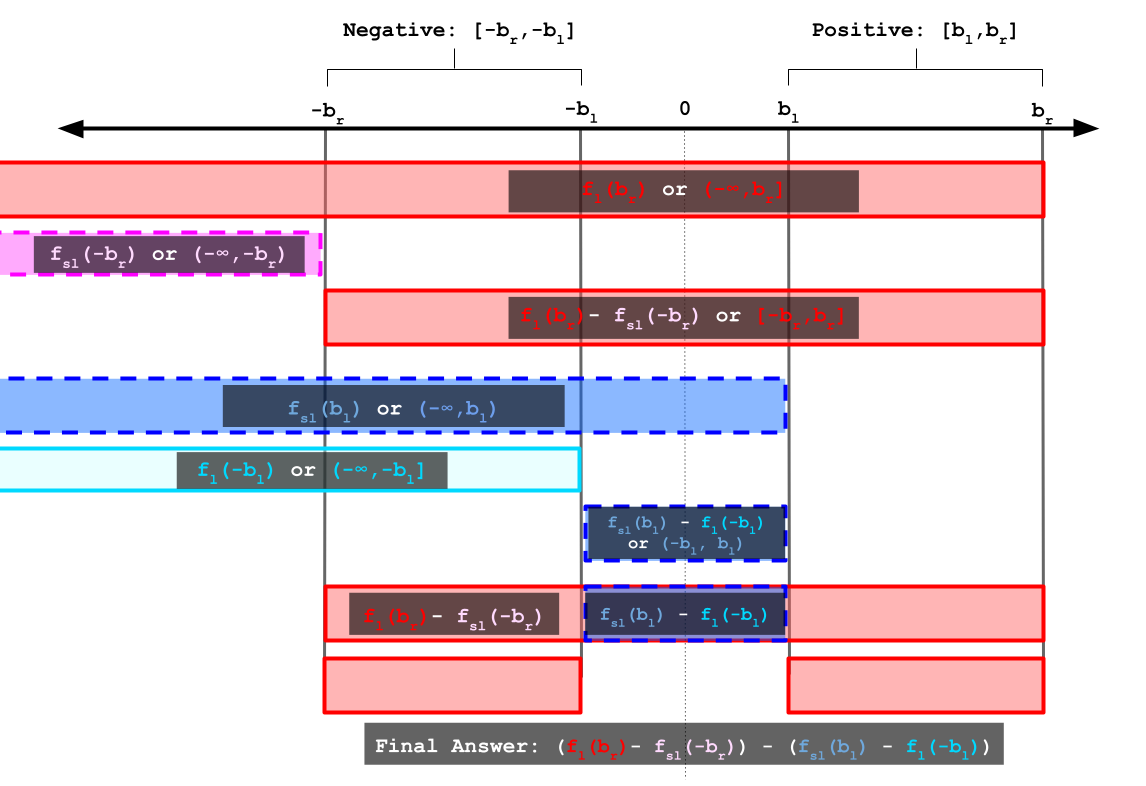
This process is displayed in the visualization below.

Putting Everything Together

Now we have the formulas for $I(S) \le K$ and $I(S) < K$ with the absolute value. The number of substrings $S$ with $I(S)$ in the range $[b_l, b_r]$ is the difference between the number of substrings with $I(S) \le b_r$ and the substrings with $I(S) < b_l$ .

The final formula for our answer is $(f_l(b_r) - f_{sl}(-b_r)) - (f_{sl}(b_l) - f_l(-b_l))$ : the subarrays in the range $[-b_r, -b_l]$ and $[b_l, b_r]$ .

Final Formula Visualization

A dotted border means exclusive range, while continuous means inclusive range.

Complexity: $\mathcal O(|T| \log |T|)$

Comments

There are no comments at the moment.