Editorial for MALD Contest 1 P6 - Scratch Cat and Painting

Remember to use this editorial only when stuck, and not to copy-paste code from it. Please be respectful to the problem author and editorialist.
Submitting an official solution before solving the problem yourself is a bannable offence.

Author: Lost

Hint 1

How can the area of the annuli/circles be approximated without cutting up both the x and y dimensions?

Hint 2

How can a Riemann sum be modified to work for circles? How can you easily extend it to work for Annuli?

Subproblem 1

Length of Union of Line Segments

To solve this problem, you must first be able to solve this subproblem. This can be done using Klee's Algorithm or coming up with your algorithm, as long as its complexity is $\mathcal O(N \log N)$ .

An alternative to Klee's algorithm is to first sort the line segments by their starting point, then for every line:

If its start point is greater than the current segment union endpoint: Add the difference of the current union end and start to our answer. Then start a new segment union by updating the union start and end variables.
If its start point is less than or equal to the segment union endpoint, the line is connected to the current segment union. Check to see if the line's endpoint is greater than the segment union's endpoint. If so, the current segment union is extended by the line, meaning we should update the current segment union endpoint. Otherwise, the line is completely covered by the current segment union.

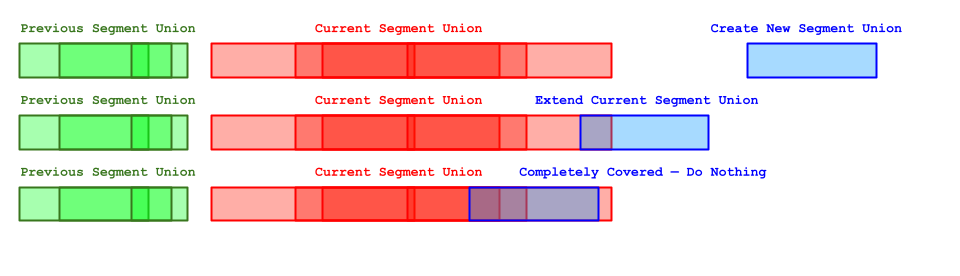
The diagram above shows the $3$ possible cases for a current line segment (blue).

This algorithm is about twice as fast as Klee's algorithm because an array of size $N$ instead of $2N$ is sorted. If you are tight on time, this algorithm can halve your runtime.

Subproblem 2

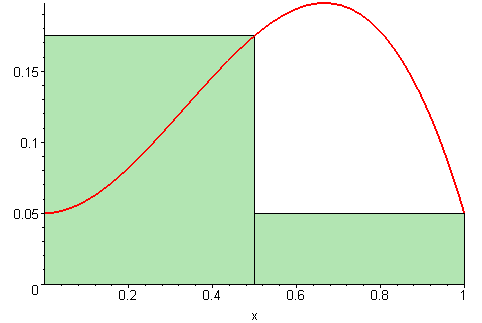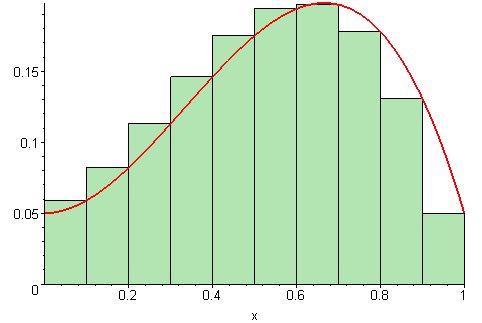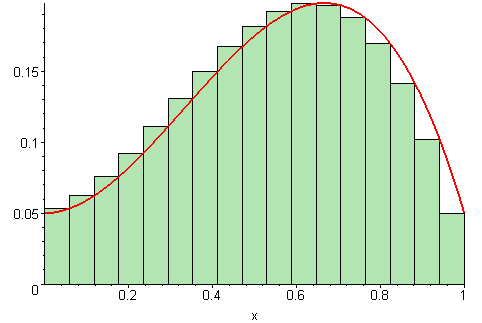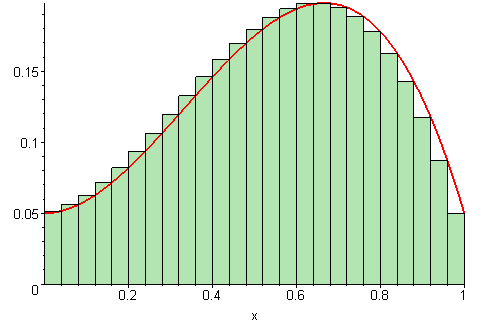
Riemann Sums: Approximating Area Under a Function

A Riemann sum is an approximation for the area between a function and the x-axis. We can modify this idea to find the area bounded by circles (or annuli) instead of a function and the x-axis. Rather than finding the area between a function and the x-axis, you can use the upper and lower y-values of the circle as a bound for rectangles.

Rectangle-Based Riemann Sums

Left Sum	Middle Sum	Right Sum

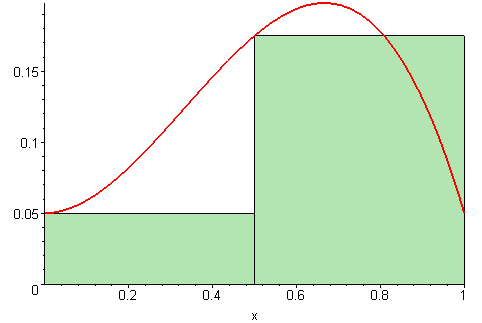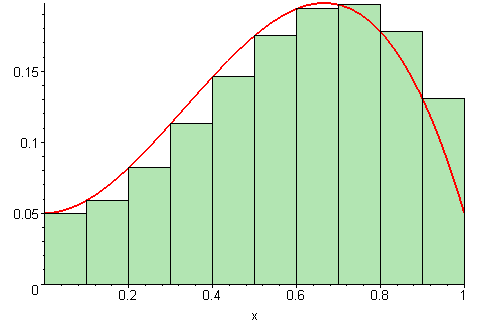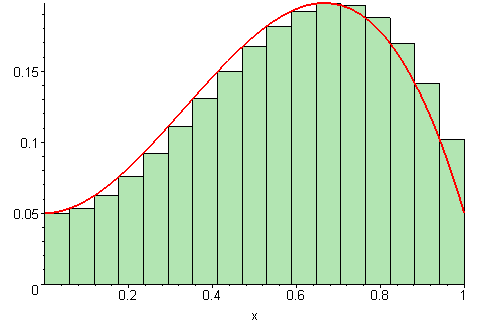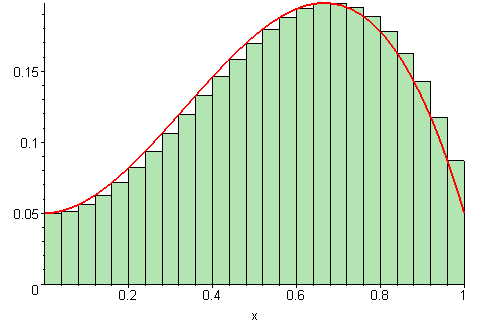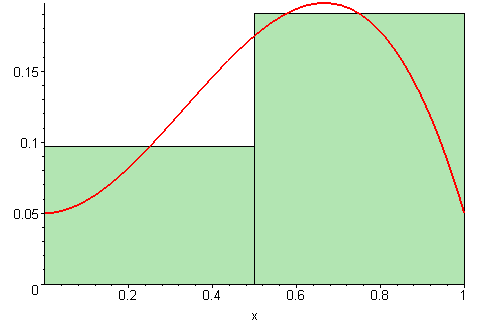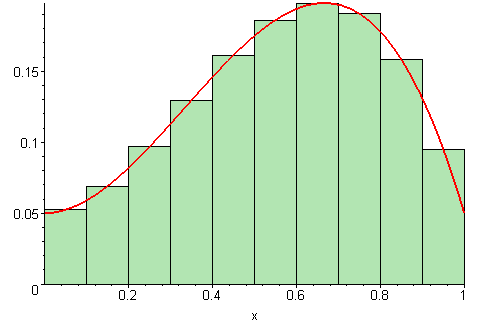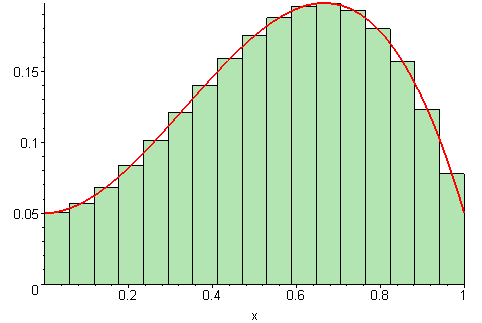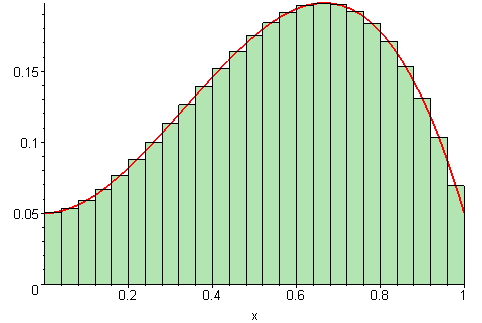Trapezoidal Sums

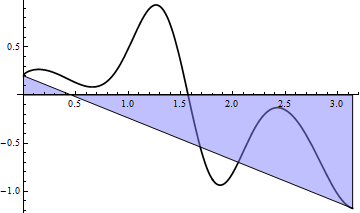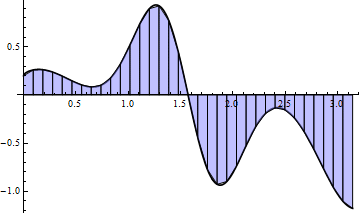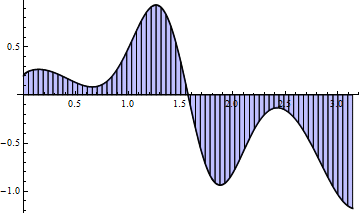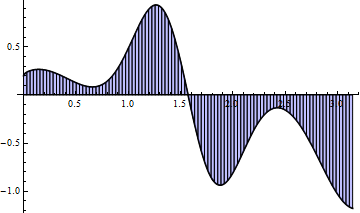
There are many Riemann sums types such as trapezoidal that achieve the same accuracy as rectangular using much fewer partitions. These are complex to modify for overlapping circles/annuli. For simplicity, use rectangle-based Riemann sums.

Full Solution

This problem is finding the area of the union of circles in subtask $1$ and annuli in subtask $2$ . Some complex solutions use multivariable calculus concepts, but $N \le 50$ and $0 \le x_i, y_i, r_i \le 1000$ , allowing us to approximate the union of circles with rectangles. We can extend this idea to work for annuli (see Fig. 1).

The general idea is to break up circles into rectangles of width $\Delta x$ . Iterate each $x$ value with increments of $\Delta x$ . For each $x$ , calculate the sum of the union of rectangle heights at $x$ and multiply it by $\Delta x$ (rectangle width). The sum the segment union areas from each partition is the total area.

Figure 1. Modified Left Riemann Sum on Three Annuli

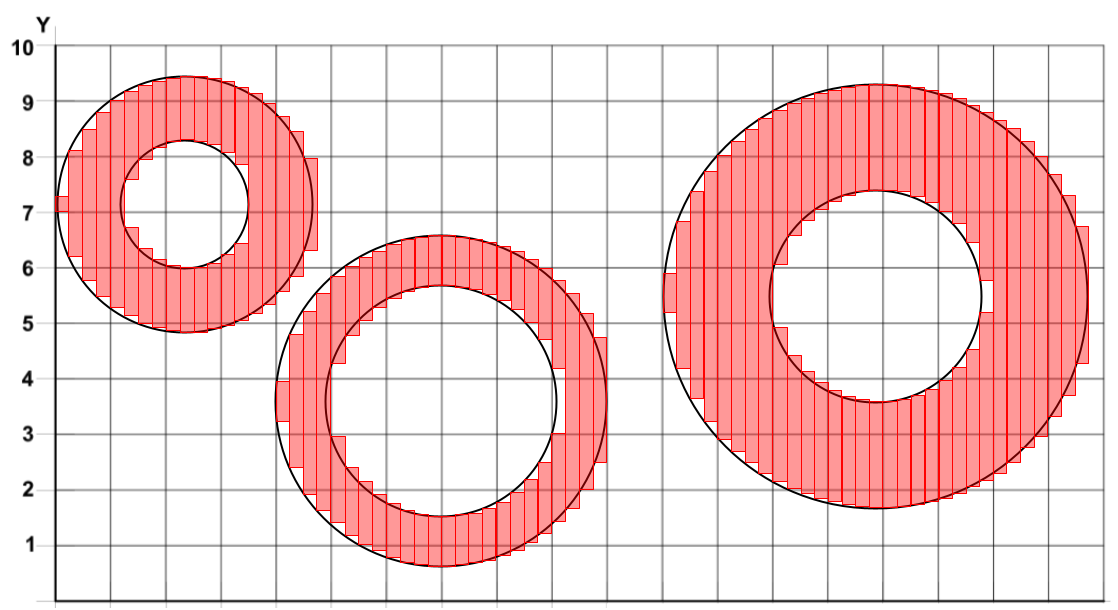
$3$ annuli with a left Riemann sum (left rectangle height is based off of function). $\Delta x = 0.25$ in this example (assuming one grid is one unit).

Figure 2. Modified Riemann Sums on Two Disjoint Unions

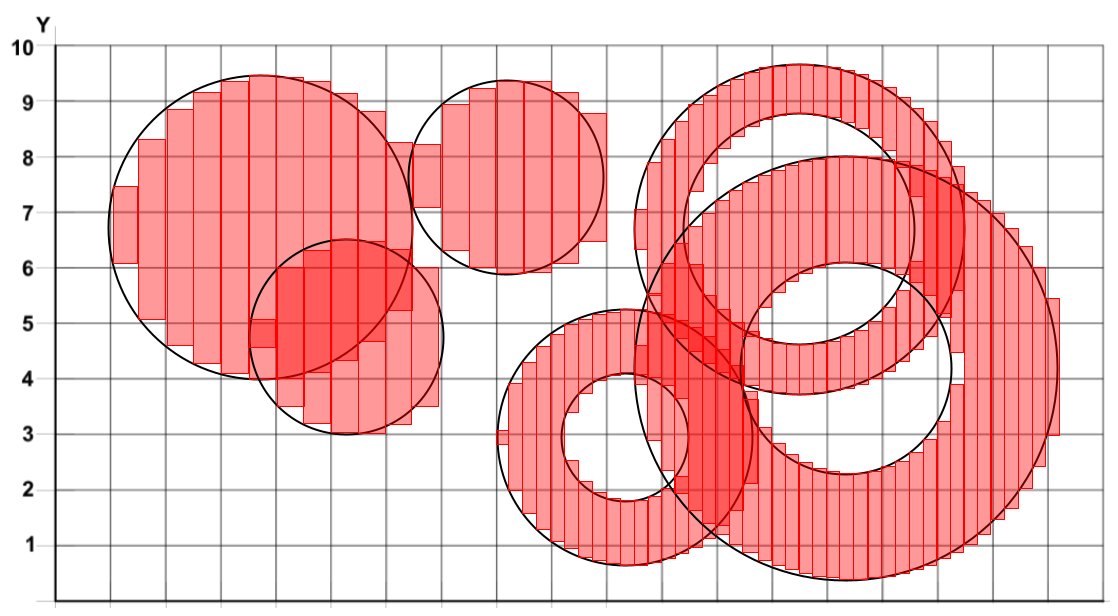
Figure 2. A circle union with $\Delta x = 0.5$ along with the $3$ annuli from Fig.1.

Figure 3. Expanded Circle Union

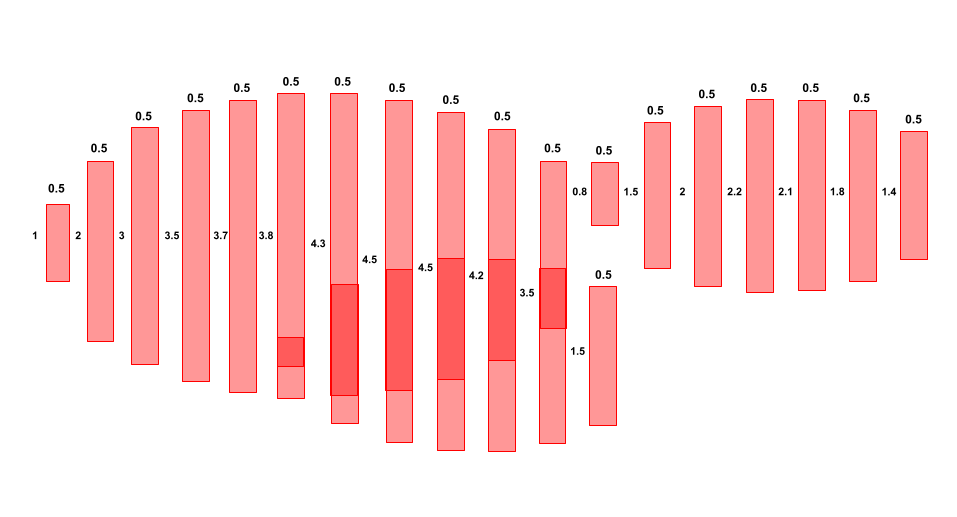
Figure 3. The rectangles from the circle union in Fig. 2 spread out with rectangle width and height displayed. Heights are completely eyeballed — just for illustration purposes.

As seen in Fig 3., you can approximate the area by partitioning the circle from its minimum $x$ ~x~ value to its maximum $x$ ~x~ value. Overlapping regions should not be overcounted, so we calculate segment union length rather than the sum of lengths.

Each rectangle height is distance between the upper and lower value of the circle. These can be found by modifying the implicit equation for a circle:

$\displaystyle (x-x_i)^2 + (y-y_i)^2 = r_i^2$ $\displaystyle (y-y_i)^2 = r_i^2-(x-x_i)^2$ $\displaystyle y = \pm \sqrt{r_i^2-(x-x_i)^2} + y_i$

For a circle, the lower bound for a rectangle is $-\sqrt{r_i^2-(x-x_i)^2} + y_i$ ~-\sqrt{r_i^2-(x-x_i)^2} + y_i~ and the upper bound is $\sqrt{r_i^2-(x-x_i)^2} + y_i$ ~\sqrt{r_i^2-(x-x_i)^2} + y_i~. Find the segment for each circle at $x$ ~x~ (if it's defined) and store them in a list. Find the length of the segment unions in the list and multiply it by $\Delta x$ ~\Delta x~ (width). An annuli can have one or two segments, either $\left[ -\sqrt{r_i^2-(x-x_i)^2} + y_i, \sqrt{r_i^2-(x-x_i)^2} + y_i \right]$ , or $\left[ -\sqrt{r_i^2-(x-x_i)^2} + y_i, -\sqrt{h_i^2-(x-x_i)^2} + y_i \right]$ and $\left[ \sqrt{h_i^2-(x-x_i)^2} + y_i, \sqrt{r_i^2-(x-x_i)^2} + y_i \right]$ .

If there are multiple disjoint unions at $x$ ~x~, you can still multiply their total sum by $\Delta x$ ~\Delta x~. This works because $(a + b + c) \times \Delta x = a \times \Delta x + b \times \Delta x + c \times \Delta x$ .

Difference Between Left and Middle Sums

If there were no intersections, there wouldn't be a large difference because circles/annuli are symmetrical; over guesses cover gaps.

For this problem, middle sums perform better due to the smaller over guesses and gaps, but it doesn't matter which one you use unless you are tight on time. In the reference solution, using middle sums allowed a $\Delta x$ value twice as large, cutting down runtime roughly in half. For every $x$ value, you should find the union sum at $x + \frac{\Delta x}{2}$ rather than at $x$ . This represents the middle of the rectangle rather than the left side.

In the reference solution, left sums was accepted a with maximum $\Delta x$ of $0.03$ , while middle sums with a maximum $\Delta x$ of $0.06$ .

Finding a $\Delta x$ ~\Delta x~ Value

One option is trial and error, but you don't need to keep submitting until your solution gets TLE or AC.

A better method is to approximate the minimum $\Delta x$ value by approximating the operations of your program.

For the intended solution, $\frac{\max x_i - \min x_i}{\Delta x} \cdot 2N \log (2N)$ can approximate the operations performed. This approximation has $2N$ instead of $N$ because there can be $2$ segments per annulus at many $x$ values and calculating segment union length also uses operations. Solving the equation $\frac{2000-(-1000)}{\Delta x} \cdot 100 \log 100 < 10^8$ gives about $\Delta x > 0.02$ . You can definitely run $10^8$ operations within the time limit.

This may not be completely accurate, but it's a good place to start. The reference solution with $\Delta x = 0.02$ runs in $0.1$ seconds with $\approx 1.01 \times 10^8$ operations. The approximation was very accurate this time, partially a coincidence and because of the simple operations in the reference solution. This $\Delta x$ value can be made roughly $20$ times smaller (especially for C++ users), considering it ran in $0.1$ seconds on its worst case. The largest $\Delta x$ value accepted on the reference solution was $0.03$ (left) or $0.06$ (middle). Depending on your implementation, you may experience different results.

Intended Complexity: $\mathcal O(\frac{\max x_i - \min x_i}{\Delta x} \cdot N \log N)$

Comments

There are no comments at the moment.