ICPC North America Qualifier 2016, Problem I

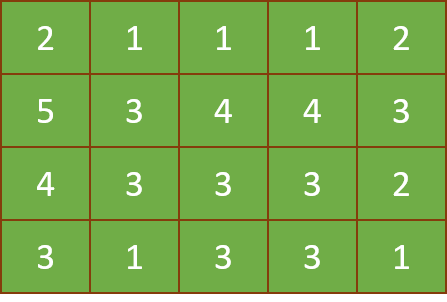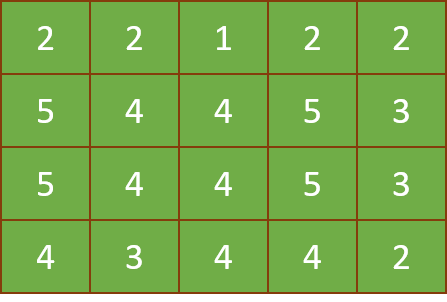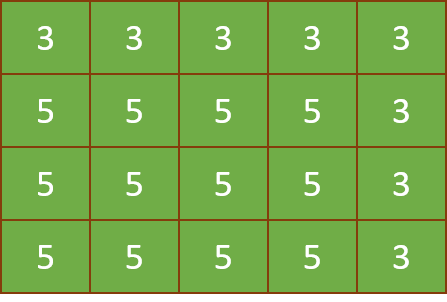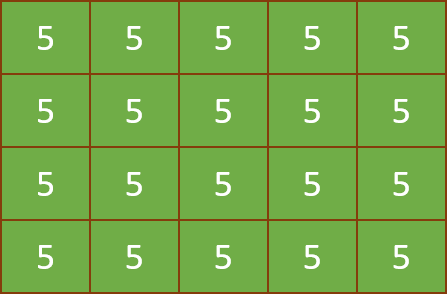
Primonimo is a game played on an ~n \cdot m~ board filled with numbers taken from the range ~1 \dots p~ for some prime number ~p~. At each move, a player selects a square and adds ~1~ to the numbers in all squares in the same row and column as the selected square. If a square already shows the number ~p~, it wraps around to 1.

The game is won if all squares show ~p~. Given an initial board, find a sequence of moves that wins the game!

Input Specification

The input consists of a single test case. The first line contains three numbers ~n\ m\ p~ denoting the number of rows ~n~ ~(1 \le n \le 20)~, the number of columns ~m~ ~(1 \le m \le 20)~, and a prime number ~p~ ~(2 \le p \le 97)~. Each of the next ~n~ lines consists of ~m~ numbers in the range ~1 \dots p~.

Output Specification

If a winning sequence of at most ~p \cdot m \cdot n~ moves exists, output an integer ~k \le p \cdot m \cdot n~ denoting the number of moves in the sequence. Then output ~k~ moves as a sequence of integers that numbers the board in row-major order, starting with ~1~. If there are multiple such sequences, you may output any one of them. If no winning sequence exists, output -1.

Sample Input 1

4 5 5
2 1 1 1 2
5 3 4 4 3
4 3 3 3 2
3 1 3 3 1

Sample Output 1

6
19 12 2 18 5 5

Sample Input 2

3 3 3
3 1 1
1 3 2
3 2 3

Sample Output 2

13
4 2 6 1 9 7 5 5 7 1 2 3 3

Sample Input 3

3 2 2
1 2
2 1
1 2

Sample Output 3

-1

Sample Input 4

3 2 2
2 1
2 1
1 1

Sample Output 4

1
6