National Olympiad in Informatics, China, 2002
The Crete islands are famously home to a society of savage cavemen. On
the islands, there are  caves arranged in a loop shape. These caves
are labeled
caves arranged in a loop shape. These caves
are labeled  in clockwise order. There are
in clockwise order. There are  cavemen
living on the island, initially located in caves
cavemen
living on the island, initially located in caves  .
Each year afterwards, the
.
Each year afterwards, the  -th caveman will move clockwise by
-th caveman will move clockwise by
 caves. Each caveman has a lifespan of
caves. Each caveman has a lifespan of  , the number of
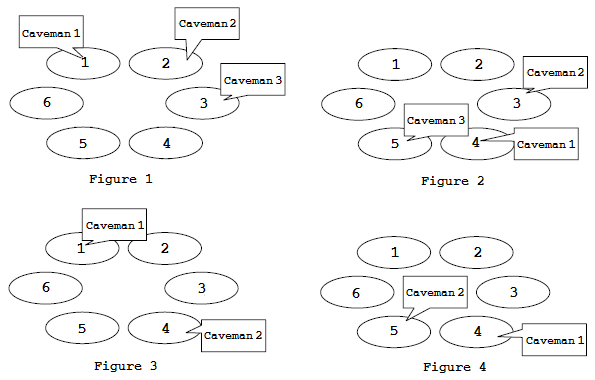
years they survive. The four figures below illustrate the scenario of an
island with six caves and three cavemen, in the span of four years. The
three cavemen initially live in the caves numbered
, the number of
years they survive. The four figures below illustrate the scenario of an
island with six caves and three cavemen, in the span of four years. The
three cavemen initially live in the caves numbered  ,
,  , and
, and  . Each
year they move by
. Each
year they move by  ,
,  , and
, and  caves, respectively. Their lifespans are
caves, respectively. Their lifespans are
 ,
,  , and
, and  , respectively.
, respectively.
What's interesting is that although there are many cavemen, no two
cavemen will ever share the same cave in any year of their lifetimes.
This ensures that the little island will always maintain its peace and
quiet, which is very puzzling for scientists. They would like to know,
what is the minimum number of caves needed for the island to maintain
its peace?
Input Specification
The first line of input contains a single integer 
 ,
the number of cavemen. Lines
,
the number of cavemen. Lines  to
to  each contain three
integers
each contain three
integers  ,
,  , and
, and  .
.  ;
;
 , representing the initial cave numbers of caveman
, representing the initial cave numbers of caveman
 , the number of caves it moves by per year, and its lifespan.
, the number of caves it moves by per year, and its lifespan.
Output Specification
Output a single integer  , the minimum number of caves required to
maintain peace. There is guaranteed to be a solution, and
, the minimum number of caves required to
maintain peace. There is guaranteed to be a solution, and  will not
exceed
will not
exceed  .
.
Sample Input
Copy
3
1 3 4
2 7 3
3 2 1
Sample Output
Copy
6
Problem translated to English by Alex.

Comments