National Olympiad in Informatics, China, 2003

This is a very ancient game. The objective is to arrange sticks on a table to create an equation that does not hold true, in a way so that if a single stick is moved, the equation will become true. Now it is your turn.

You are given one equation that is guaranteed to not hold true. If it is possible to make the equation true by moving a single stick, then output the new equation. Otherwise, output No.

The following rules and constraints hold for the equation:

1. The equation may contain positive or negative numbers. The only operators will be the plus sign and the minus sign. There will only be one equal sign.
2. The equation will not contain numbers with ~10~ or more digits (all operands will be less than or equal to ~999\,999\,999~ in absolute value).
3. You may only move sticks used to construct numbers, not sticks used for the operators (+, -, =). Therefore the plus, minus, and equal signs will not change. Before and after moving a stick, the arrangements of each digit must strictly correspond to that of figure 2.
4. There will not be leading zeros for numbers in the initial equation, but leading zeros in numbers after moving a stick is permitted.

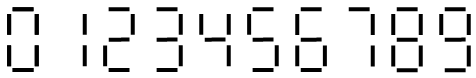
Input Specification

The input will contain one equation on a single line, followed by the single character # (ASCII code 35). There will not be spaces or other separator characters within the equation. The length of the equation will be less than or equal to 1000 characters. Note: After the # character, there may be characters that are irrelevant to the problem.

Output Specification

The output should contain one line, the corrected equation, in the same format as the input (terminated with a #, with no extra characters anywhere in the output). If a solution does not exist, output No.

Sample Input 1

1+1=3#

Sample Output 1

1+1=2#

Sample Input 2

1+1=3+5#

Sample Output 2

No

Sample Input 3

11+77=34#

Sample Output 3

17+17=34#

Problem translated to English by Alex.