National Olympiad in Informatics, China, 2009

We are given a special kind of binary search tree. By definition, the key of any node in the binary search tree is strictly greater than the key of the node's left child, but is strictly less than the key of the node's right child.

On the other hand, each node of the binary search tree has a priority, where the priority of each node is strictly less than the priority of the node's children.

It is already known that all of the node keys in the tree are distinct, and that all of the node priorities in the tree are also distinct. Now we arrive at an interesting conclusion: if we can determine the keys and priorities of all the nodes in the tree, then the structure of the tree can also be determined. This is because we can think of this tree as one that's constructed by inserting all of the nodes in order of ascending priority, where the binary search tree nodes are compared by their keys.

We define the depth of a node in the tree as its distance from the root node plus ~1~. Thus, the root node itself will have a depth of ~1~.

Other than a key and a priority, each node also has an access frequency. We define a node's access cost within the tree to be its access frequency multiplied by its depth. The access cost of the entire tree is defined as the sum of the access costs amongst all its nodes.

Now, given each node's key, priority, and access frequency, you may modify the priority of some number of nodes at an additional modification cost of ~K~ for each node's priority changed. You may change the priority of nodes to any real number, but the change must ensure that the priorities of all the nodes afterwards remain distinct. The problem you must solve is, determine the minimum possible sum of the entire tree's access frequency and the total modification cost.

Input Specification

The first line of input contains two integers ~N~ and ~K~. ~N~ is the number of nodes and ~K~ is the modification cost for each priority value changed.
The next line contains ~N~ nonnegative integers, the keys of all the nodes.
The next line contains ~N~ nonnegative integers, the priorities of all the nodes.
The next line contains ~N~ nonnegative integers, the access frequencies of all the nodes.
None of the keys, priorities, and access frequencies in the test data will exceed ~400\,000~. Pairs of adjacent values on the same line will be separated by a single integer, and there will not be any trailing spaces.

Output Specification

The output should consist of one line containing a single number, the minimum possible value achievable for the sum of the entire tree's access cost and the total modification cost.

Sample Input

4 10
1 2 3 4
1 2 3 4
1 2 3 4

Sample Output

29

Explanation

The left diagram below depicts the original tree in the sample input. Its overall access cost is ~1 \times 1 + 2 \times 2 + 3 \times 3 + 4 \times 4 = 30~. The optimal modification scheme is to change the priority of node 3 to 0, obtaining the right diagram below. The new overall access cost is ~1 \times 2 + 2 \times 3 + 3 \times 1 + 4 \times 2 = 19~. Plus a single additional modification cost of 10, the minimum possible sum becomes 29. (Note from translator: the value in the upper box of a node is the key, and the value in the lower box is the priority.)

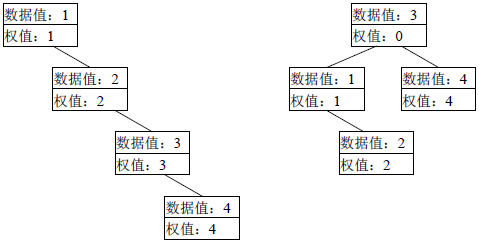
Constraints

40% of the test cases satisfy ~N \le 30~.
70% of the test cases satisfy ~N \le 50~.
100% of the test cases satisfy ~N \le 70~ and ~1 \le K \le 30\,000\,000~.

Problem translated to English by Alex.