NOI '10 P3 - Altitude
View as PDFNational Olympiad in Informatics, China, 2010
City YT is a well-designed city. The main roads that run east-west and
north-south divide the city into regions. Simply put, we can
view city YT as a square with each region also being a square. From
this, we know that city YT contains
intersections
and
bidirectional streets (simply referred to as
streets). Each street connects a pair of intersections on a main road.
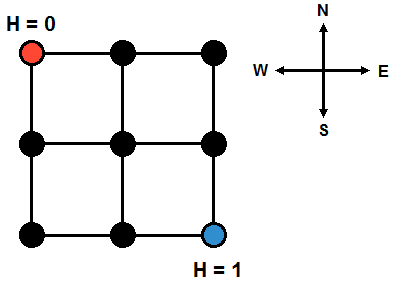
The diagram below depicts a map of city YT
divided into
regions, including
intersections and
streets.
Little Z is the mayor of this city. Using statistical information, he
has obtained the bidirectional flow rate of people in each street during
rush hours. For the duration of each rush hour, he will know the number
of people going in a specific direction on a specific street. Each
intersection also possesses an altitude, which is an issue that
citizens of city YT find very stressful. For a person to climb up to an
altitude of will require him to exhaust
units of energy. If
going downhill, no energy will be required. When traveling along a
street, if the difference between the destination altitude and the
initial altitude is
(note that
can be negative), then a person
will consume
units of energy when traveling along the
street (here,
represents the largest of two numbers
and
).
Little Z also measured the altitude of the intersection at the
north-west corner of city to be , and the altitude of the intersection
at the south-east corner to be
(as depicted in the above diagram).
However, there is no way to determine the altitudes of other
intersections. Little Z would like to know in the most ideal situation
(where you can freely assume altitudes for any intersection), what is
the minimum total energy consumed by people climbing the slopes during
rush hour?
Input Specification
The first line of input consists of a single integer , the meaning of
which is described above.
For the following lines, each line contains a nonnegative
integer representing the number of people (i.e. the flow rate) passing
through a particular street in a particular direction during rush
hour.
The input order is: numbers representing the flow rates of
people going from west to east, followed by
numbers
representing the flow rates of people going from north to south,
followed by
numbers representing the flow rates of people
going from east to west, finally followed by
numbers
representing the flow rates of people going from south to north. For
each directional flow rate, the input order will be from north to south
according to initial locations. If the north-south position of the
initial locations are the same, then the input order will be from west
to east (see sample below).
Output Specification
Output a single number, the minimum possible total energy consumption of all people traveling during rush hour if the altitudes were ideal. Round the answer (half-up) to the nearest integers.
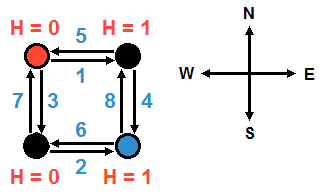
Sample Input
1
1
2
3
4
5
6
7
8Sample Output
3Explanation
The following diagram depicts the scenario in the sample above. It also indicates the altitudes in an ideal situation.
Constraints
For of the test cases:
.
For of the test cases:
.
For of the test cases:
.
For of the test cases:
, and
.
Also, all flow rates will be integers.
Hint
Altitudes may not necessarily be integers.
Problem translated to English by .
Comments