Warning: The original problem has a 2GB memory limit, but DMOJ only supports a 1GB memory limit. Solutions exist using less than 1GB of memory.

There are ~n~ worms numbered from ~1~ to ~n~. The length of a worm can be represented by a positive integer between ~1~ and ~6~. You want to arrange the worms into several queues. Initially, each worm is in its own queue with only one worm (itself). Each worm is both at the front and at the end of its queue.

There are ~m~ operations. Each operation is one of the following three types:

• 1 i j where ~1 \leq i,j \leq n~: Merge the queue worm ~i~ is in with the queue worm ~j~ is in. In the new queue, worm ~j~ will be immediately after worm ~i~ (and for the rest of the worms, the worm before/after them remains unchanged). It is guaranteed that worm ~i~ is at the tail of some queue , worm ~j~ is at the front of some queue, and ~i,j~ are not in the same queue.
• 2 i where ~1 \leq i \leq n~: Split the queue between worm ~i~ and the worm immediately after ~i~. It is guaranteed that worm ~i~ is not at the tail of some queue.
• 3 s k where ~k~ is a positive integer and ~s~ is a numeric string with length at least ~k~: Find the product of ~f(t)~ modulo ~998\,244\,353~ where ~t~ is over all substrings of length ~k~ in ~s~. There are ~|s| - k + 1~ such substrings ~t~ given ~s~ and ~k~.

The definition of ~f(t)~ is given below.

For a given queue, the ~k~-string after worm ~i~ is obtained by starting from worm ~i~, walking towards the tail of the queue, and finding the ~k~ nearest worms to ~i~, including ~i~, and concatenating the lengths of these worms. If there are fewer than ~k~ worms before reaching the tail, then worm ~i~ won't have a ~k~-string. For example, if the numbers of worms in a queue are ~10,22,3~ and they have lengths ~4,5,6~; then the 3-string after worm ~10~ is ~456~, worm ~22~ does not have a 3-string, but its 2-string is ~56~ and its 1-string is ~5~.

~f(t)~ denotes the number of worms whose ~k~-string is exactly ~t~.

Input Specification

The first line consists of two positive integers ~n,m~ denoting the number of worms and the number of operations.

In the second line, there are ~n~ positive integers not exceeding ~6~ denoting the length of worm ~1,\ldots,n~.

In the following ~m~ lines, each line specifies an operation.

The input file might be large.

Output Specification

For each operation 3 s k, output a line with an integer denoting the output.

Sample Input 1

5 9
3 1 3 5 3
3 333135 2
3 333135 1
1 1 3
1 2 5
1 3 2
1 5 4
3 333135 2
3 333135 1
3 333135 3

Sample Output 1

0
81
1
81
0

Explanation for Sample 1

For the first query, since there is only one worm in each queue, no worms have a 2-string, so the output is simply ~0~.

For the second query, each worm's 1-string is the string formed by the worm's own length, so we see the 1-strings are ~1,3,3,3,5~ (in no particular order) and the output is ~f(3) \cdot f(3) \cdot f(3) \cdot f(1) \cdot f(3) \cdot f(5) = 81~.

Sample Input 2

2 10
6 6
3 666666 1
1 1 2
3 666666 2
3 666666 4
3 666666666666666666666666666666 1
2 1
1 2 1
3 666666 2
3 666666 4
3 666666666666666666666666666666 1

Sample Output 2

64
1
0
75497471
1
0
75497471

Explanation for Sample 2

For the 4th and the 7th query, since ~s~ is ~30~ 6s, ~f(t)~ is ~f(t) = 2^{30}~. Output it modulo ~998\,244\,353~.

Additional Samples

queue.zip

Constraints

~n \leq 2 \times 10^5, m \leq 5 \times 10^5, k \leq 50~.

Let ~\sum |s|~ denote the sum of lengths of ~s~ in all queries. ~\sum |s| \leq 10^7~.

Let ~c~ denote the number of operations of the form 2 i, then ~c \leq 10^3~.

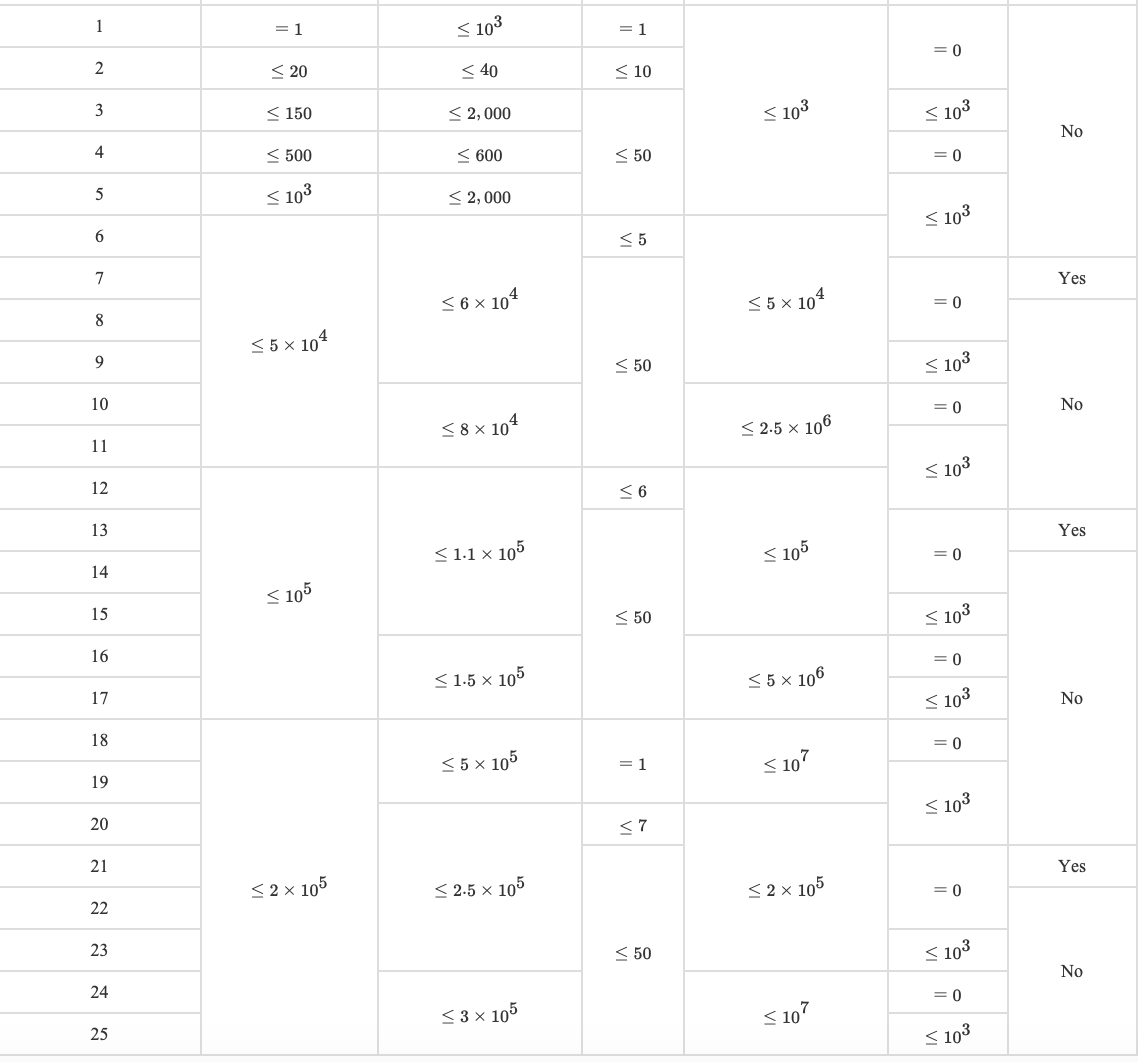
The columns, from left to right, are:

• Test case
• ~n~
• ~m~
• ~k~
• ~\sum |s|~
• ~c~
• Whether all lengths and all query strings ~s~ are formed by 1s.