Description

There are ~n~ clones of Little P on the plane. Define the area occupied by a group of instances as the smallest convex polygon that covers this group of instances. Little P has limited abilities, and some clones will disappear every moment. But before the next moment, Little P will use the magic technique to make these disappeared clones reappear in their original positions.

Given ~m~ queries, after each moment when the clone disappears, what is the area occupied by the remaining clone?

Input Specification

The first line of input contains two positive integers ~n,m~, describing the number of clones at the beginning and the total number of quries.

The next ~n~ line, the ~i~ line has two integers ~x_i, y_i~ , describing the position of the ~i~th clone.

In the next ~m~ lines, the first integer ~k~ in each line indicates that ~k~ clones have disappeared at this moment. Next there are ~k~ non-negative integers ~c_1, c_2, \ldots, c_k~, which are used to generate the numbers of the disappeared clones.

Generated as follows:

Assume twice the area occupied by the avatar at the previous moment is ~S~. Then the numbers of the clones ~p_1, p_2, \ldots , p_k~ that disappeared at this moment are: ~p_i = [(S + c_i) \bmod n] + 1~.

In particular, at the first moment, we believe that ~S = -1~ in the previous moment, that is: the numbers of the clones ~p_1, p_2, \ldots , p_k~ that disappeared at the first moment are: ~p_i = [(-1 + c_i) \bmod n] + 1~.

Output Specification

Output the ~m~ lines sequentially in the order of the given time, each line is an integer, representing twice the area occupied by the remaining clones at that time.

Sample Input

6 2
-1 0
-1 -1
0 -1
1 0
0 1
0 0
3 1 3 6
2 0 1

Sample Output

3
2

Explanation for Sample Output

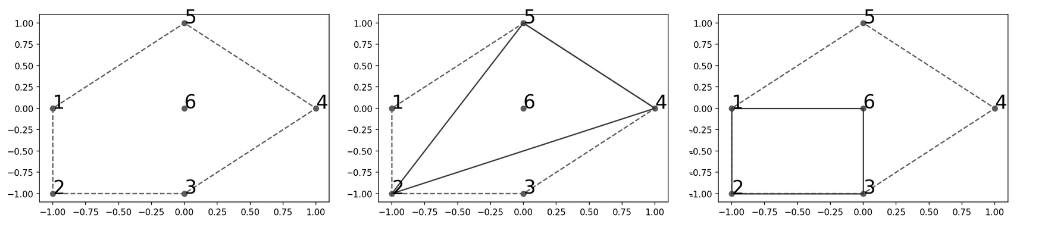
As shown in the figure below: the left picture shows the positions of the input ~6~ clones and the area they occupy; the middle picture shows the situation at the first moment, the numbers of the disappeared clones are ~1, 3,~ and ~6~ respectively, and the remaining ~3~ points occupy the inner area of the solid line in the picture, which is twice the area of ~3~; the right picture shows the situation at the second moment, and the numbers of the disappeared clones are respectively

~[(0 + 3)\bmod 6] + 1 = 4~

~[(1 + 3)\bmod 6] + 1 = 5~

The remaining ~4~ points occupy the area inside the solid line in the graph.

Constraints

For all data, it is guaranteed that:

• ~|x_i|,|y_i|\le 10^8~;
• No two clones have exactly the same coordinates;
• ~k\le 100~;
• The sum of ~k~ at all times does not exceed ~2\times 10^6~;
• ~0\le c_i\le 2^{31}-1~;
• Initially, all ~n~ clones occupy an area greater than ~0~;
• The set of vertices defining the region occupied by all ~n~ clones is ~S~ , ~|S|\ge 3~ . At any moment, there are at least two undisappeared clones in ~S~.