Your code will be run through three extra samples. These sample files can be found here.
In this problem, a tree is defined recursively: a single node gives
rise to a tree, letting a tree to be the left (or right) child (of the
root node) gives rise to a tree, and letting two trees to be left and
right children (of the root node) gives rise to a tree. All structures
generated using the above three rules in finite steps are called
trees. In other words, the "tree" here refers to a non-empty, rooted
binary tree that distinguishes left children and right children.
Two trees  ,
,  are said to be isomorphic (
are said to be isomorphic ( ) if they
meet one of the following four conditions: (1) trees that are formed by
one node are isomorphic; (2) if the root nodes of
) if they
meet one of the following four conditions: (1) trees that are formed by
one node are isomorphic; (2) if the root nodes of  and
and  have only
the left child, and their left subtrees are isomorphic, then
have only
the left child, and their left subtrees are isomorphic, then  and
and
 are isomorphic; (3) if the root nodes of
are isomorphic; (3) if the root nodes of  and
and  have only the
right child, and their right subtrees are isomorphic, then
have only the
right child, and their right subtrees are isomorphic, then  and
and  are isomorphic; (4) if the root nodes of
are isomorphic; (4) if the root nodes of  and
and  have both the left
and right children, their left subtrees are isomorphic, and their right
subtrees are also isomorphic, then
have both the left
and right children, their left subtrees are isomorphic, and their right
subtrees are also isomorphic, then  and
and  are isomorphic. In other
words, two trees are isomorphic if and only if they are the same when the
nodes are unlabeled but we are distinguishing left children and right
children.
are isomorphic. In other
words, two trees are isomorphic if and only if they are the same when the
nodes are unlabeled but we are distinguishing left children and right
children.
It is obvious that the isomorphism of trees forms an equivalence relation
over all trees, and we treat isomorphic trees as the same. We say two
trees are different if and only if they are not isomorphic.
A leaf of a tree is defined in the usual way: a leaf is a node
without any children.
We say  may be converted to
may be converted to  using a single-step substitution
if we may replace a leaf node of
using a single-step substitution
if we may replace a leaf node of  with another tree
with another tree  and the
resulting tree is isomorphic to
and the
resulting tree is isomorphic to  , and we use
, and we use  to
denote
to
denote  may be converted to
may be converted to  using a single-step substitution. We
say
using a single-step substitution. We
say  may be converted to
may be converted to  by substitution if there exists a
natural number
by substitution if there exists a
natural number  and trees
and trees  such that
such that
 . We use
. We use
 to denote
to denote  may be converted to
may be converted to  by substitution.
by substitution.
In other words, a single-step substitution means we are deleting a leaf
of the tree and putting a new tree at the corresponding position, just like
a larger subtree growing at the original leaf node. If a tree  may be
converted to another tree
may be
converted to another tree  by substitution, then it just means we
may use zero, one, or multiple rounds of single-step substitutions to
convert
by substitution, then it just means we
may use zero, one, or multiple rounds of single-step substitutions to
convert  into
into  . For example, any tree may be converted to
itself by substitution, or in other words, for any tree
. For example, any tree may be converted to
itself by substitution, or in other words, for any tree  , we
have
, we
have  . This figure shall help understand the meaning
of substitution and single-step substitution:
. This figure shall help understand the meaning
of substitution and single-step substitution:
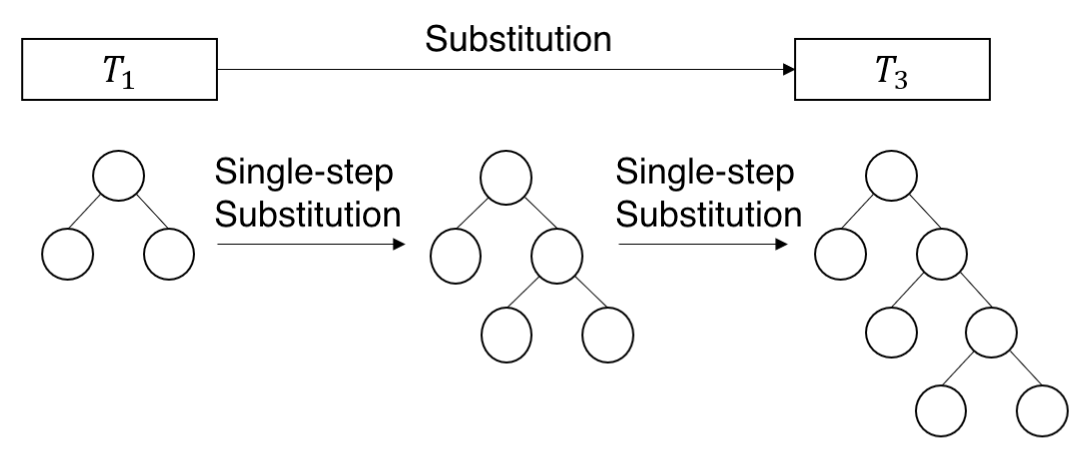
In particular, we can convert any tree into infinitely many different
trees by substitution, and a tree formed by a single node can be
converted to any other tree by substitution. For a tree  , we define
, we define
 to be the set of trees that we may convert
to be the set of trees that we may convert  into by
substitution, or in other words,
into by
substitution, or in other words,
 . Moreover, if
. Moreover, if
 is a finite set of trees, then
is a finite set of trees, then
 is defined to be the union of
is defined to be the union of  where
where
 . So we have
. So we have
 .
.
We may treat  as the set of trees the trees in set
as the set of trees the trees in set
 can grow into. In other words, the set of trees that trees
in
can grow into. In other words, the set of trees that trees
in  can grow into includes all trees that may be converted
into from some
can grow into includes all trees that may be converted
into from some  by substitution. We may call a set of
trees a forest. Not rigorously speaking, the new forest that a given
forest can grow into are all the trees in the given forest and all
possible trees that a tree in the given forest may grow into. It is
obvious that the forest a non-empty forest can grow into is an infinite
forest, but the infinite forest, or in other words,
by substitution. We may call a set of
trees a forest. Not rigorously speaking, the new forest that a given
forest can grow into are all the trees in the given forest and all
possible trees that a tree in the given forest may grow into. It is
obvious that the forest a non-empty forest can grow into is an infinite
forest, but the infinite forest, or in other words,  ,
does not necessarily contain all the trees. Moreover, it does not have
to contain "nearly all" trees.
,
does not necessarily contain all the trees. Moreover, it does not have
to contain "nearly all" trees.
We say a forest is almost complete (or in other words, contains almost
all trees) if there are only finitely many trees are not in the forest.
For a finite forest  ,
,  may contain all
trees, contain almost all trees, or there are infinitely many trees not
in the forest. For a given finite set of trees
may contain all
trees, contain almost all trees, or there are infinitely many trees not
in the forest. For a given finite set of trees  , there
exists an efficient algorithm to decide whether
, there
exists an efficient algorithm to decide whether  is
almost complete, i.e., there are only finitely many trees that trees in
is
almost complete, i.e., there are only finitely many trees that trees in
 cannot grow into.
cannot grow into.
The problem asks given a finite set of trees  , whether
there exists only finitely many trees
, whether
there exists only finitely many trees  satisfying
satisfying
 .
.  simply means
there does not exist a
simply means
there does not exist a  such that
such that
 .
.
Input Specification
Each test case contains multiple instances. The first line
contains a positive integer  . There are
. There are  instances following, and
each instance is specified in the following format: the first line is an
integer
instances following, and
each instance is specified in the following format: the first line is an
integer  denoting the number of trees in the set. We will specify the
denoting the number of trees in the set. We will specify the
 trees using the following format: the first line is an integer
trees using the following format: the first line is an integer  denoting the number of nodes in the tree. The nodes are numbered
denoting the number of nodes in the tree. The nodes are numbered
 . The following
. The following  lines contain two non-negative
integers each, and the
lines contain two non-negative
integers each, and the  -th line contains
-th line contains  separated by a
space denoting the left child and the right child of node
separated by a
space denoting the left child and the right child of node  . If the
left or the right child does not exist, then
. If the
left or the right child does not exist, then  or
or  is equal to
is equal to  .
Of course, the leaf nodes satisfy
.
Of course, the leaf nodes satisfy  . The input
guarantees that it will be a tree with node
. The input
guarantees that it will be a tree with node  being the root. Please
note that the labels of the nodes are for convenience only, and
isomorphic trees are considered to be the same.
being the root. Please
note that the labels of the nodes are for convenience only, and
isomorphic trees are considered to be the same.
There may be isomorphic trees in the  trees of an instance. If we
remove the duplicate trees (i.e. we only keep one tree for each
isomorphism class), they shall form a set
trees of an instance. If we
remove the duplicate trees (i.e. we only keep one tree for each
isomorphism class), they shall form a set  . You need to
decide whether
. You need to
decide whether  is almost complete.
is almost complete.
Output Specification
The output contains  lines specifying the answers to the
lines specifying the answers to the
 instances. The
instances. The  -th line contains a string: if in the
-th line contains a string: if in the  -th
instance, the
-th
instance, the  trees in the input grow into an almost complete forest
(or in other words, there are only finitely many trees the trees
specified in the instance cannot grow into), output
trees in the input grow into an almost complete forest
(or in other words, there are only finitely many trees the trees
specified in the instance cannot grow into), output Almost Complete.
Otherwise, output No. Please pay attention to spelling and
capitalization.
Sample Input 1
Copy
1
1
1
0 0
Sample Output 1
Copy
Almost Complete
Sample Input 2
Copy
1
3
3
2 3
0 0
0 0
2
2 0
0 0
2
0 2
0 0
Sample Output 2
Copy
Almost Complete
Sample Input 3
Copy
1
2
3
2 3
0 0
0 0
2
2 0
0 0
Sample Output 3
Copy
No
Explanation for Sample Output 3
It is obvious for all  chain-looking trees such that every
non-leaf node has only the right child are not in
chain-looking trees such that every
non-leaf node has only the right child are not in  ,
and so there are infinitely many trees not in
,
and so there are infinitely many trees not in  .
.
Constraints
For all test cases,
 ,
,  ,
,  ,
,  .
Here,
.
Here,  denotes the sum of numbers of nodes of the
trees in the instances occurring in a test case,
denotes the sum of numbers of nodes of the
trees in the instances occurring in a test case,  denotes the sum of number of trees occurring in the instances in a test
case,
denotes the sum of number of trees occurring in the instances in a test
case,  denotes the maximum height of trees occurring in the
particular test case (a tree with only one node has height 1).
denotes the maximum height of trees occurring in the
particular test case (a tree with only one node has height 1).
| Test case |
 |
 |
 |
 |
Additional Constraints |
| 1 |
 |
 |
 |
None. |
| 2 |
 |
For each instance,  , or in other words, there are at most 4 trees in the set of trees occurring in the instance. , or in other words, there are at most 4 trees in the set of trees occurring in the instance. |
| 3 |
| 4 |
 |
 |
None. |
| 5 |
 |
For each instance, the trees in the set have the same height. |
| 6 |
 |
None. |
| 7 |
 |
For each instance, the trees in the set have the same height. |
| 8 |
 |
None. |
| 9 |
 |
For each instance, the trees are chains (i.e. any non-leaf node has only one child). |
| 10 |
 |
 |
 |
 |
For each instance, there are only trees satisfying one of the following two conditions
(1) any non-leaf node has only one child
(2) there are exactly two leaf nodes, and they have the same parent. All other nodes have exactly one child. |
| 11 |
 |
| 12 |
 |
| 13 |
 |
| 14 |
 |
 |
 |
None. |
| 15 |
 |
 |
 |
| 16 |
 |
| 17 |
 |
 |
| 18 |
 |
| 19 |
 |
| 20 |
 |
| 21 |
 |
| 22 |
 |
| 23 |
| 24 |
| 25 |

Comments