NOIP '07 P4 - Core of a Tree Net
View as PDFLet be an acyclic and connected undirected graph (also known as an unrooted tree), each edge has a positive integer weight, we call
a tree network, where
Respectively represent the collection of nodes and edges,
represents the collection of the length of each side, and let
have n nodes.
Definitions
Path: There is a unique simple path between any two nodes
and
in the tree network. Let
represent the length of the path with a and b as the endpoints, which is the sum of the lengths of the sides on the path. We call
the distance between two nodes
. The distance from a point
to a path P is the distance from that point to the nearest node on P:
Diameter of the tree network: The longest path in the tree network is called the diameter of the tree network. For a given treenet
, the diameter is not necessarily unique, But it can be proved that the midpoint of each diameter (not necessarily exactly a certain node, it may be inside a certain side) is unique, and we call this point the center of the tree network.
Eccentric distance
: the distance from the node farthest from the path
in the tree network T to the path
, that is
Task
For a given tree network and a non-negative integer
, find a path
, which is a path on a certain diameter (both ends of the path are nodes in the tree network) , whose length does not exceed
(can be equal to
), so that the eccentricity
is the smallest. We call this path the core of the tree network
. When necessary,
can degenerate to a node. Generally speaking, under the above definition, there is not necessarily only one core, but the minimum eccentricity is unique.
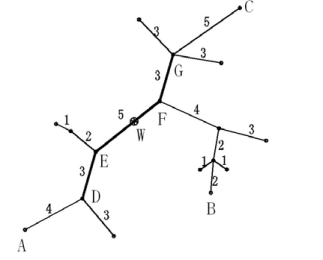
The figure below shows an example of a tree network. In the figure, and
are two diameters with a length of 20. Point
is the center of the treenet, and the length of the
edge is
. If
is specified, the core of the tree network is path
(or path
), and the eccentricity is
. If
(or
or
), the core of the tree network is node
with an eccentricity of
.
Input Specification
- Line
, two positive integers
and
, separated by a space.
is the number of nodes in the tree network, and
is the upper bound of the length of the core of the tree network. Let the node numbers be
.
- Lines
to
each contains 3 positive integers separated by spaces, indicating the two endpoint numbers and length of each edge in turn. For example,
2 4 7means that the length of the edge connecting nodesand
is
.
It's guaranteed that the input forms a valid tree.
Output Specification
One non-negative numbers, the minimum eccentricity under this condition.
Sample Input 1
5 2
1 2 5
2 3 2
2 4 4
2 5 3Sample Output 1
5Sample Input 2
8 6
1 3 2
2 3 2
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3Sample Output 2
5Constraints
of the test cases satisfy
.
of the test cases satisfy
.
of the test cases satisfy
,
.
of the test cases satisfy
,
, and all lengths are positive integers not exceeding
.
of the test cases satisfy
,
, and all lengths are positive integers not exceeding
.
Comments