Little E fell in love with a game called "Meow Meow". This game has a pile of cards and $n$ stacks that allow bottom deletions. The task is to eliminate all the cards through the game rules.

At the beginning, there are $m$ cards in the deck, having patterns $a_1,a_2,\dots ,a_m$ from top to bottom. All cards have a total of $k$ patterns, numbered from $1$ to $k$. For each pattern, the number of cards with it in the deck is even. All stacks are empty at the beginning. There are two operations in this game:

• Choose a stack and put the top card of the deck on top of the stack. If after doing this, the top two cards of the stack have the same pattern, these two cards will be eliminated automatically.
• Choose two different stacks. If the cards at the bottom of the two stacks have the same pattern, these two cards can be eliminated, and the card above the bottom of the stack will become the new bottom of the stack. If different, nothing will be done.

There are a total of $T$ levels in this game, and little E has been unable to pass the level. Please help Little E design a game plan, that is, for each level of the game, give the corresponding operation sequence so that Little E can eliminate all the cards.

Input Specification

The first line contains a positive integer $T$ representing the number of data sets.

Next, there are $T$ sets of data, in each set of data:

• The first line contains three positive integers $n$, $m$, $k$, which respectively represent the number of stacks, the number of cards, and the type of pattern on the card.
• The second line contains $m$ positive integers, representing $a_1,a_2,\dots ,a_m$, respectively, representing the pattern of the cards in the deck from top to bottom.

The input data is guaranteed to have a solution.

Output Specification

For each set of data, output several lines.

The first line contains a positive integer $\mathit{op}$, indicating the number of operations. You need to guarantee that $m\le op\le 2m$.

For the next $\mathit{op}$ lines, each line contains two or three positive integers separated by a space.

• If two integers 1 $s$, do the first operation once and select stack $s$.
• three integers 2 $s_1$ $s_2$, do a second operation and select stacks $s_1$ and $s_2$.

You need to guarantee that $1\le s,s_1,s_2\le n$, and $s_1\ne s_2$.

Sample Input 1

1
2 4 2
1 2 1 2

Sample Output 1

5
1 1
1 1
1 2
2 1 2
1 1

Explanation of Sample 1

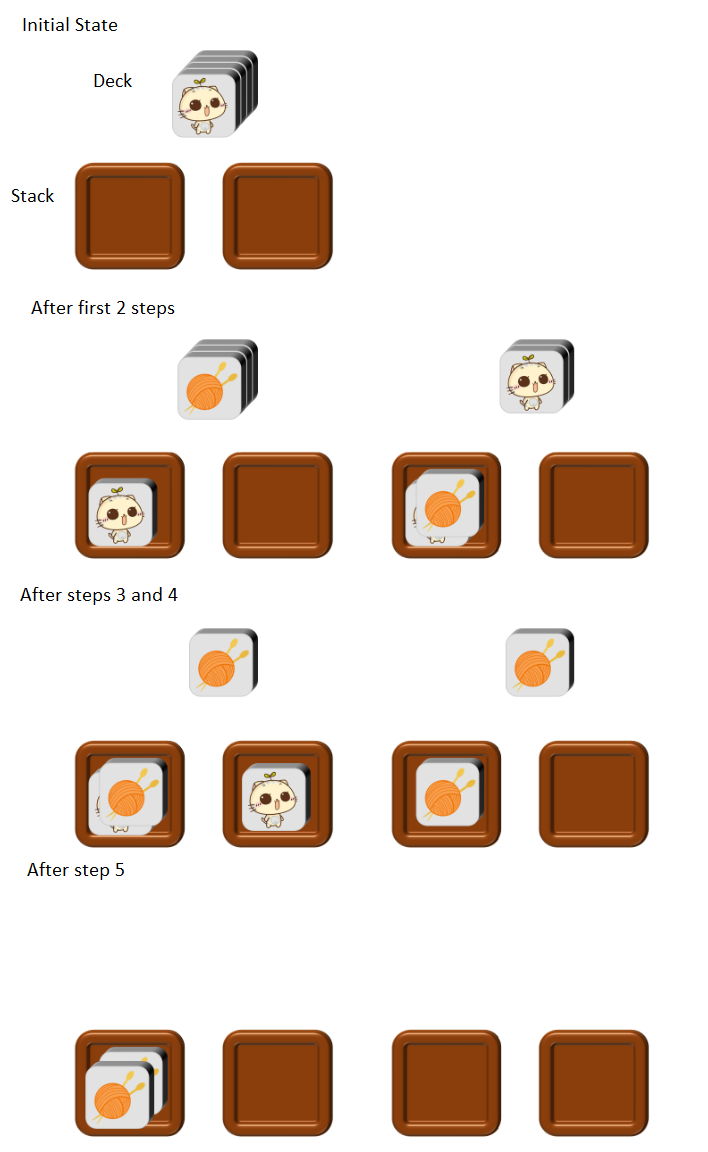
Additional Samples

Additional sample cases can be found here. Included is a grader meow_e.cpp.

Constraints

Let $S$ be the total of $m$ across all $T$ testcases.

For all data, guarnatee $S\le 2\times {10}^6$, $n\le 300$, $1\le a_i\le k$.

Case	$T$	$n$	$k$	$m$
$1-3$	$1001$	$\le 300$	$2n-2$	no additional constraints
$4-6$	$1002$	$=2$	$2n-1$
$7-10$	$3$	$=3$		$\le 14$
$11-14$	$1004$			no additional constraints
$15-20$	$1005$	$\le 300$

Note that you can use the value of $T$ to distinguish the type of data.