Build walls between vertices to form a single enclosed fence without crossings or branches. The number indicates exactly how many walls — according to the crazy city building laws — must surround it (and a lack of number means there's no constraint.) So, presented with the following ~5 \times 5~ grid of land squares:

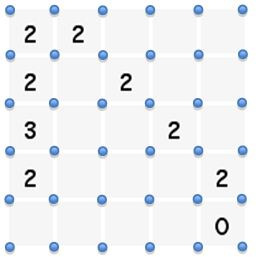
the following fence could be constructed:

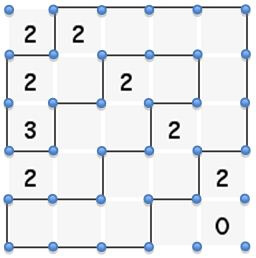
The grid of lots is always ~r \times c~, where ~1 \le r, c \le 20~ (we actually don't know what's the largest ~c~ that can be done in a second, so will keep on cranking it up as better solutions come in and update: current max ~c~ is 6), and each lot is either a number (0, 1, 2, or 3) to impose a constraint, or a blank if no constraint is being imposed. You're to output the length of the longest possible loop (or equivalently, the number of vertices in the loop), or -1 if no loop exists. Note that loops of length 0 are invalid. A valid loop must enclose a non-zero amount of area.

Subtasks

There are currently 6 subtasks present. Subtask ~N~ contains only tests where ~c = N~. You will receive ~N^3~ marks for solving subtask ~N~. To get credit for subtask ~N > 1~, you must correctly solve subtask ~N-1~.

The data currently consists of just the original data used at the ICPC regional, which had the added constraint that ~r = c~, though this is not an important constraint for the problem.

Input Specification

The input is one zombie fencing problem, expressed by ~r~ and ~c~, the dimensions of the problem, followed by an ~r \times c~ grid with the number constraints (with the - to represent no constraint).

Output Specification

You should print the length of the longest fence loop that can be constructed for that problem while still respecting all constraints, or you should print -1 if the problem has no such solution.

Sample Input 1

2 2
22
22

Sample Output 1

8

Sample Input 2

5 5
----0
2---2
3--2-
2-2--
22---

Sample Output 2

32