You stumble across the ruins of an ancient castle...

The ruins of the castle have left a strange pillar formation behind. In particular, there are $N$ adjacent pillars each with height $h_i$. Let $x$ represent your exhaustion. It initially starts at $1$, and increases by $1$ after each time you jump to a taller pillar. It takes $x$ seconds to travel from pillar $i$ to pillar $i+1$ if $h_i\ge h_{i+1}$. However, there are $2$ different ways to travel to a taller pillar.

1. You can run across pillar $i$ in $x$ seconds and then climb up to pillar $i+1$ in $x(h_{i+1}-h_i)$ additional seconds.
2. You can jump directly from pillar $i$ to pillar $i+1$ in $x$ seconds. You can jump as high as you want, but jumping will exhaust you.

Given this information, what is the lowest amount of time needed to get from pillar $1$ to pillar $N$?

Constraints

$2\le N\le 2\times {10}^5$

$1\le h_i\le {10}^9$

Subtask 1 [40%]

$2\le N\le 2000$

$1\le h_i\le {10}^5$

Subtask 2 [60%]

No additional constraints.

Input Specification

The first line of input contains an integer $N$.

The second line of input contains $N$ space separated integers representing $h_i$, the height of each pillar.

Output Specification

Output a single integer, the lowest achievable time in seconds.

Sample Input

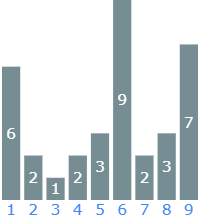
9
6 2 1 2 3 9 2 3 7

Sample Output

14

Sample Input Visualized