SMAC 08/09 (Oct) #5 - Crossroads
View as PDFSane's Monthly Algorithms Challenge: October 2008
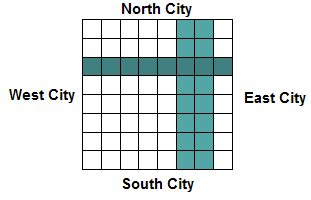
A flat rectangular grid of land separates four cities. Each city is situated on a different edge of the rectangle.
The four cities now wish to be joined by exactly roads so that
citizens may travel freely to and from each city. One road will join the
North and South cities. Another road will join the West and East cities.
The two roads will, of course, intersect somewhere, permitting anyone to
travel to and from all four cities. Each road is a solid rectangle of any
width, with sides parallel to
and
axis.
The land separating the cities is a grid of non-negative integers.
Each value represents the cost of paving a road over the cell. To pave
an entire road, all covered cells are paved and paid for exactly once.
When paving the second road, the intersection does not need to be paved
a second time.
If the roads are larger, more cars can travel from city to city. Therefore, you wish to maximize the total number of paved cells. However, you can not exceed the budget allocated for this job.
Determine the maximum number of cells which can be paved to build
exactly roads within the provided budget.
Input Specification
The first line contains integers ,
and
.
The next lines contain
non-negative integers each
,
representing the cost of paving a road over that cell.
Output Specification
A single integer representing the largest possible area which can be
paved with the given budget. If it is impossible to build both roads,
output 0.
Sample Input 1
7 5 30
0 4 0 5 5 8 9
1 1 3 2 2 3 4
0 1 2 1 4 1 1
2 9 1 4 5 3 6
7 7 1 2 4 9 7Sample Output 1
17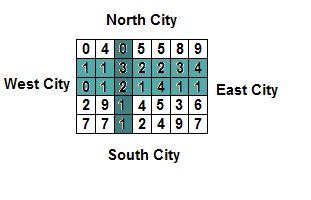
Sample Input 2
8 8 145
1 5 2 3 3 8 0 1
0 6 6 7 2 5 4 9
6 5 1 1 1 2 3 4
4 3 1 2 1 5 6 0
9 8 1 4 2 1 8 3
3 2 7 1 8 9 3 5
5 5 6 0 1 3 0 7
1 0 8 3 3 2 5 1Sample Output 2
44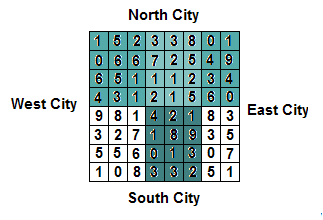
Comments