TLE '16 Contest 2 P5 - Thanksgiving Feast
View as PDF
It is almost Thanksgiving at Pierre Elliott Trudeau High School! (The school celebrates it around 1-2 weeks after the actual date). In order to truly celebrate Thanksgiving, TSAC (Trudeau Student Activity Council) has decided to host a huge Thanksgiving feast.
students (numbered from
to
) will eat at the feast. There are
chairs bolted in place, lined up in a row; each chair will be occupied by a single student. There are also
dishes (numbered from
to
); dishes can only be placed directly in front of a chair and exactly one dish must be placed in front of a chair.
Each student has a list of dishes that they would like to eat from. In particular, the student wants to eat from
specific dishes. When the feast begins, all of the students begin eating and they must reach out their arms for the various dishes around them. Students will always reach straight for a dish (i.e. they will not bend their arm around anything). However, it is considered to be uncivil if two or more students might cross their arms when getting their food. Note that arms do not cross at the dishes themselves, meaning that multiple students can eat from the same dish.
You have been tasked to choose the order to place the students and the dishes. Can you find a way to order the students and dishes so that it is impossible for any two students to cross their arms?
Constraints
For all subtasks:
The sum of all will not exceed
.
Subtask 1 [25%]
Subtask 2 [25%]
Additionally, if there is a solution, it is possible to place the dish directly in front of the
chair. In other words, if any solution exists, at least one solution will have the order of the dishes as
.
Subtask 3 [50%]
Input Specification
The first line will contain .
lines of input follow. The
line will first contain an integer,
, the number of dishes the
student wants.
space-separated integers will follow, specifying the dishes that the
student would like to eat from, in increasing order.
Output Specification
If there is a way to arrange the students and the dishes such that no two students can cross their arms, output two lines of space-separated integers each: the order of the students on the first line and the order of the dishes on the second line. If there are multiple answers, output any one of them.
If there is no valid arrangement, output every man for himself!.
Sample Input 1
2
2 1 2
1 1Sample Output 1
1 2
2 1Explanation for Sample Output 1
If the dishes are ordered 1,2 and the ordering of the students is 1,2, the two students would cross arms if student 1 reaches for dish 2 at the same time student 2 reaches for dish 1.
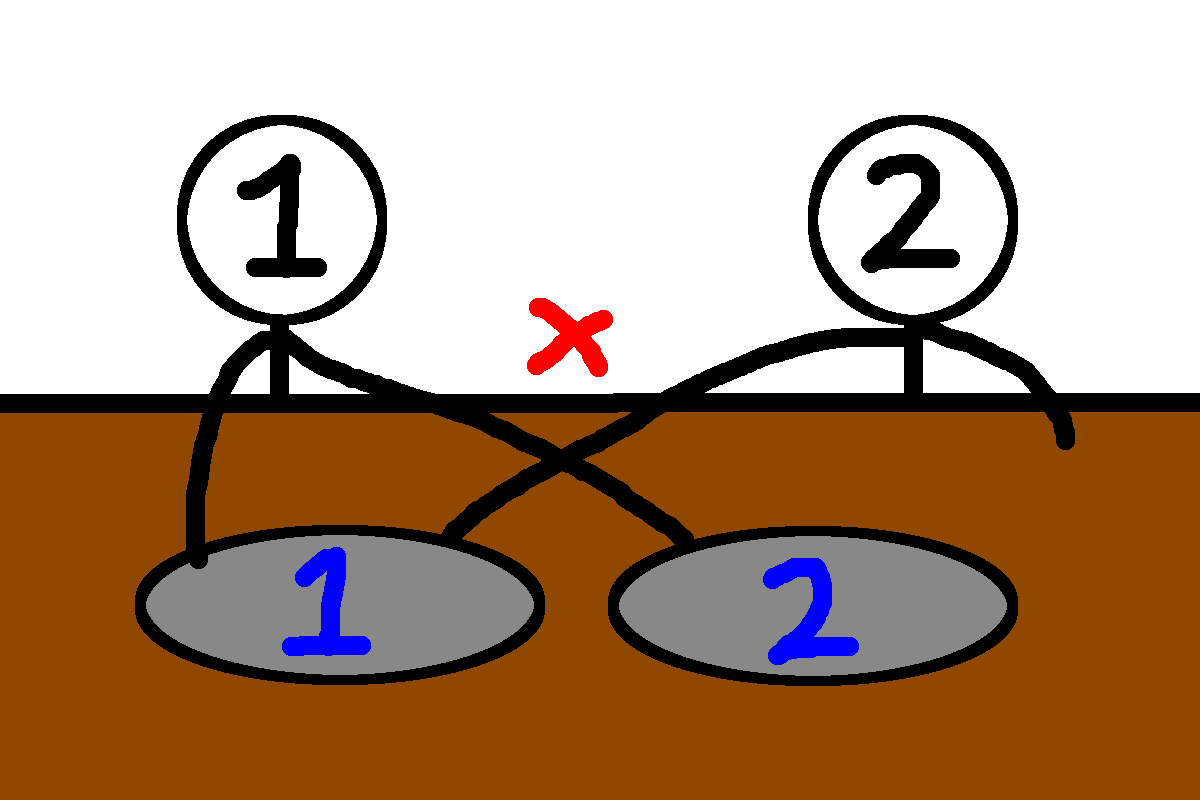
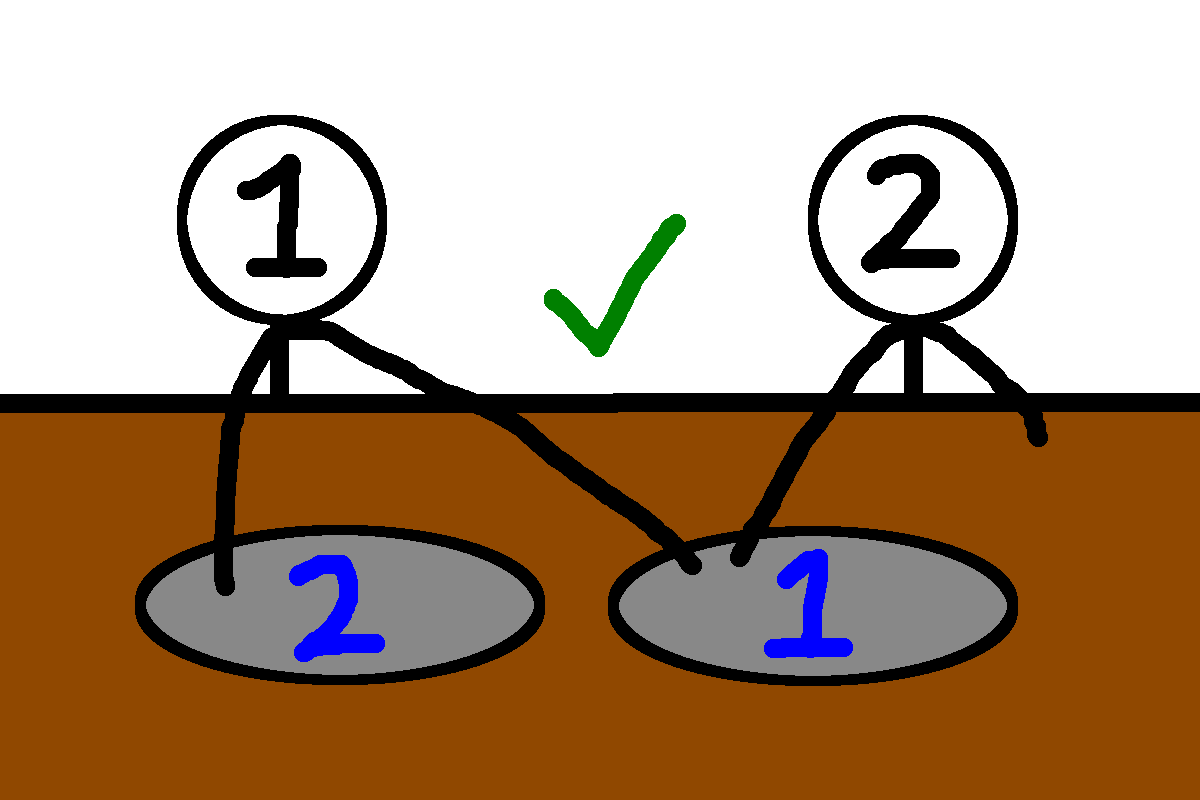
If the dishes are ordered 2,1 and the ordering of the students is 1,2, the two students will never be able to cross arms. Note that the two students are allowed to reach for dish 1 at the same time.
Sample Input 2
3
2 2 3
2 1 3
2 1 2Sample Output 2
every man for himself!Sample Input 3
3
1 1
2 1 2
2 1 3Sample Output 3
2 1 3
2 1 3
Comments
what is a WA (Presentation Error)???
It can mean one of many things.
Of course, outputting
every man for himself!bypasses these checks.