UACC 1 P4 - Converging Streams
View as PDF
In the flourishing land of Unionville, many streams flow from the mountains to nourish the village below. At various points, a stream may diverge into two, or two streams may converge into one. This occurs at exactly junction points numbered from
to
. Connecting each of these junction points are
stream segments, the
of which directs
% of the water in junction
into junction
.
Recently, some of the junctions have become polluted! Water at every junction has a measurable pollution value, which begins at at the source and increases by
upon reaching junction
. When water from two streams mix at a converging junction, the pollution values from each stream are averaged, weighted proportionally based on the volume of water in each stream, before
is added to the pollution value.
Until the pollution is cleaned up, the village chief needs to decide the safest places to source water for agriculture. Please help him determine the average pollution value of the water at each junction.
Constraints
All water starts at a single diverging source junction, which can flow to every other junction.
It is impossible to start at a junction, travel any number of streams, and return to the same junction.
The volume of water at every junction is guaranteed to be greater than .
Input Specification
The first line contains two integers, and
.
The of the following
lines contain three integers,
and
, and
.
The next line contains integers,
.
Output Specification
Output lines, the
line of which contains a real number denoting the average pollution value at the
junction. Your answer will be considered correct if it is within an absolute or relative error of
.
Sample Input
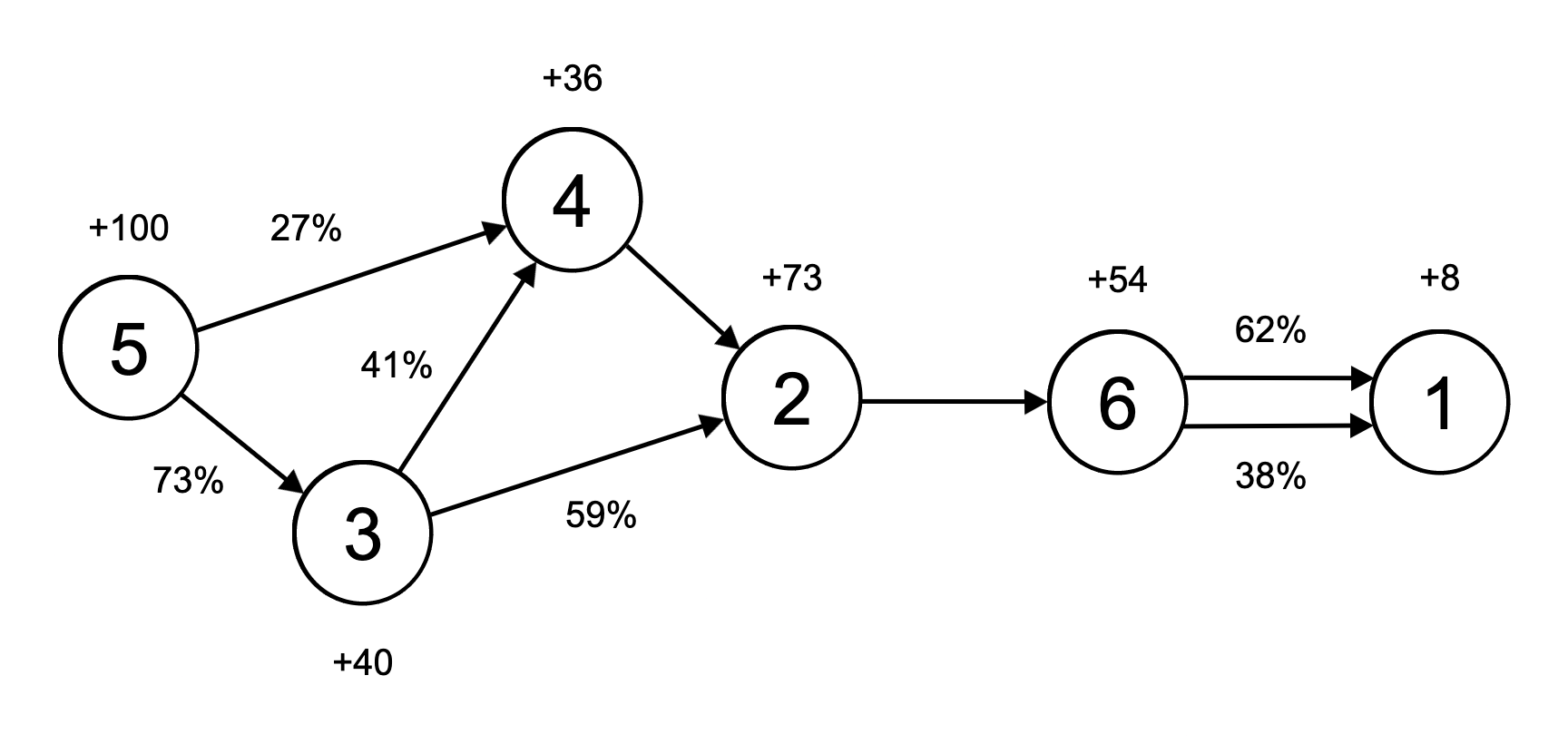
6 8
2 6 100
3 4 41
3 2 59
4 2 100
5 4 27
5 3 73
6 1 62
6 1 38
8 73 40 36 100 54Sample Output
284.6948
222.6948
140
157.029334270156
100
276.6948Explanation for Sample Output
The river system looks like this:
Comments