UACC 1 P6 - Labyrinth Treasure
View as PDF
Bob the archaeologist is searching for a treasure in a mysterious labyrinth! The labyrinth consists of rooms numbered
to
, which are connected by exactly
bidirectional corridors of varying length. The
corridor connects rooms
and
and takes
seconds to traverse. It is guaranteed that every room is reachable from any other room.
Hidden around these rooms are mysterious locked boxes, numbered
to
. The
box can be found in room
and contains exactly
keys. The
key in the
box can open box
. The treasure is located in box
.
Bob starts in room with
keys, which can open the boxes
. Since Bob is infinitely intelligent and efficient, he will always take the optimal route to obtain the treasure. Is it possible for Bob to open the box with the treasure, and if so, what is the minimum number of seconds it will take him to do so?
Constraints
Every room is reachable from every other room.
Subtask 1 [20%]
Subtask 2 [80%]
No additional constraints.
Input Specification
The first line contains the integer , the number of rooms.
The of the following
lines contains the integers
,
, and
, representing the two ends of each corridor and the time it takes to traverse it.
The next line contains two integers, and
, the number of mysterious boxes and the box the treasure is located in.
The next line contains integers,
, the rooms each box is located in.
The of the following
lines contain the integer
, followed by
integers
. These denote the number of keys contained in each box and the box that each key opens.
The next line contains the integer , the number of keys that Bob starts with.
The last line contains integers,
, the boxes that Bob can open with each of the starting keys.
Output Specification
If it is possible to open the box with the treasure, output the minimum number of seconds it will take Bob to do so. Otherwise, output .
Sample Input
10
6 1 4
4 8 10
4 6 3
5 8 7
2 7 8
8 9 2
6 10 9
1 3 4
9 2 4
10 3
5 3 5 6 2 9 10 3 4 5
3 2 8 10
1 10
0
2 5 7
1 1
2 7 8
3 3 3 10
1 3
2 2 6
1 3
2
6 6Sample Output
70Explanation for Sample Output
The rooms and boxes are arranged like this:
'' represents box
with keys to boxes
. '
' represents box
with the treasure.
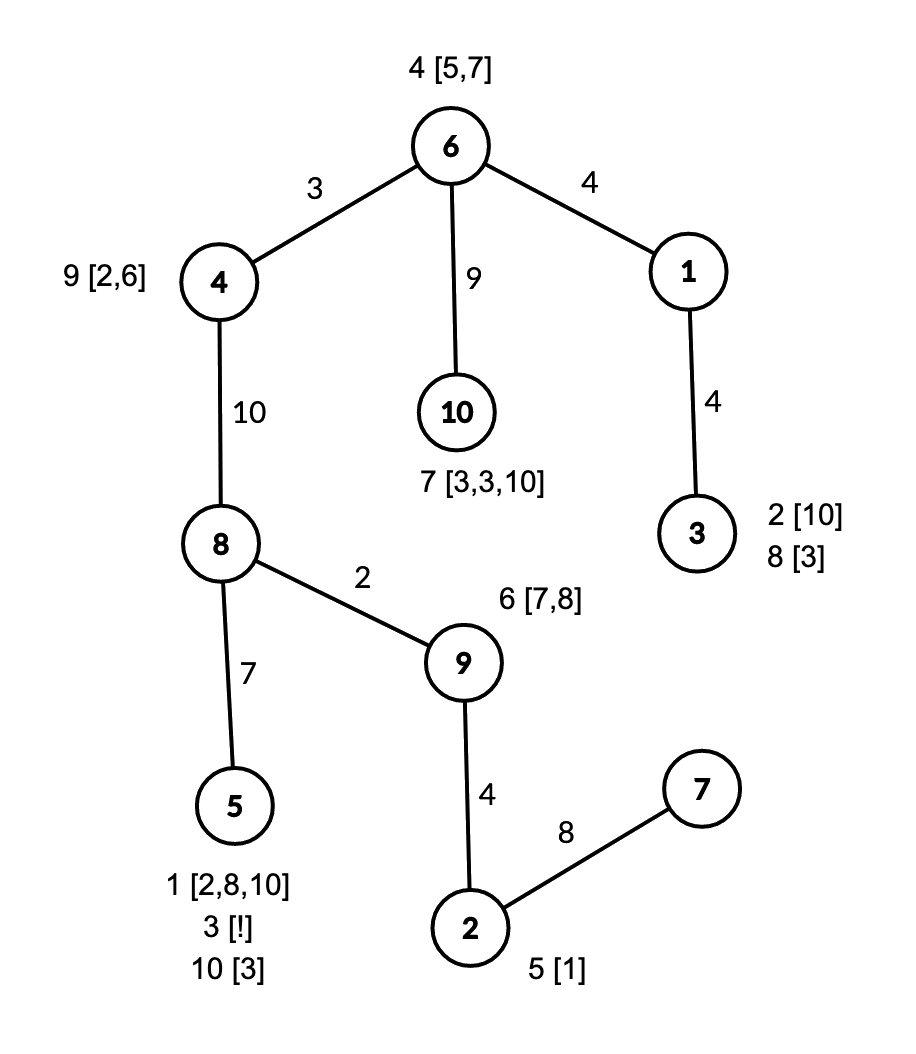
Bob can go to from room to room
to open box
, obtaining keys to boxes
and
after
seconds.
He can then go from room to room
to open box
, obtaining a key to box
after an additional
seconds.
He can then go from room to room
to open box
, obtaining the treasure after an additional
seconds.
The total time taken is seconds. It can be proven that this is the minimum time.
Comments