UCC Coding Competition '21 P5 - Woodcutting Game
View as PDFAfter tearing down your pig barn, you and your friend Tyler have to dispose of two long rectangular wooden boards. You have to cut the boards into smaller pieces. Because this is boring, you devise a game to play to make things more interesting.
The two
You and Tyler will take turns cutting the rectangular boards, and you will go first. Each of the cuts you make must turn one rectangular board into two smaller rectangular boards, each with an integer height and width. The cuts must be made either horizontally or vertically.
In particular, when it is your turn, you have two options as follows. Note that both options leave your opponent with two rectangles, so the game can continue.
Option 1: Choose one board to discard entirely, and then cut the other board into two smaller integer-dimension rectangles however you want.
The below diagram illustrates this option (but does not include all possible ways to cut the rectangle).
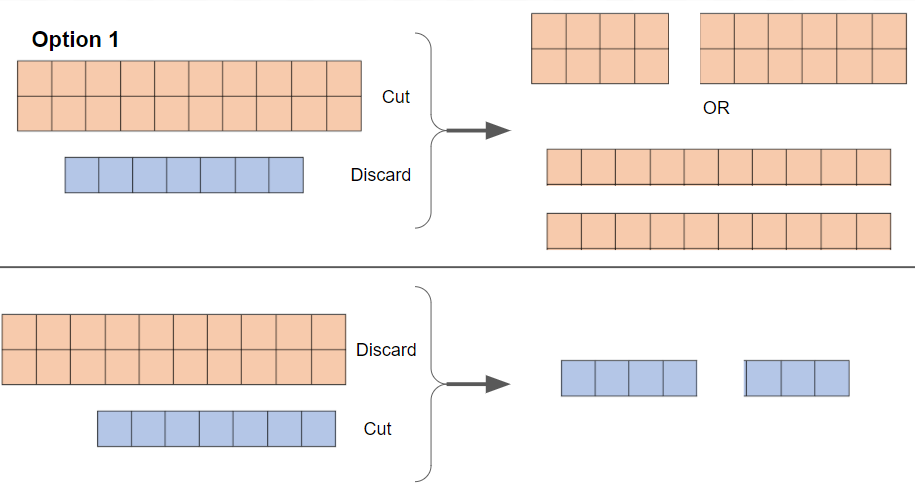
Option 2: Choose one board to leave untouched, cut a rectangular piece off the other board, and discard that piece.
If you choose Option
The below diagram illustrates this option (but does not include all possible ways to cut the rectangle).
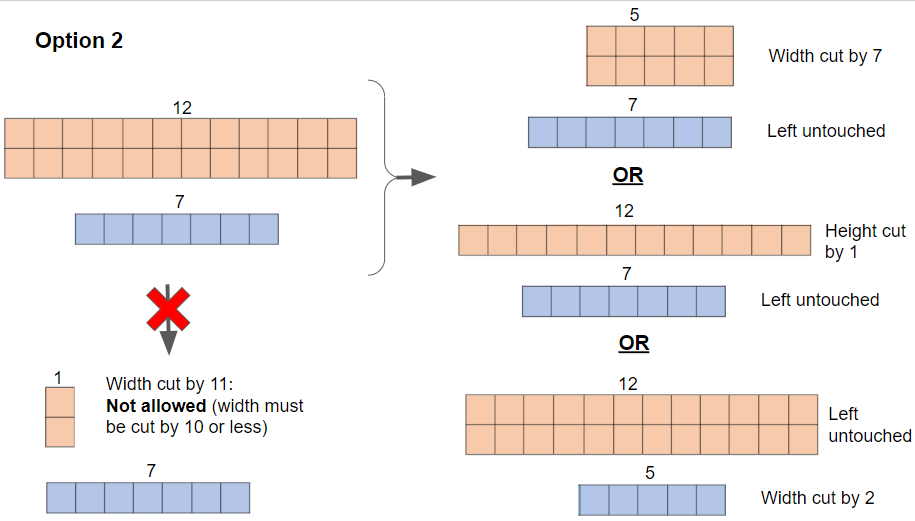
You move first. The player who leaves the other player with two
You are deciding whether to place a bet against Tyler, so you want to know whether it is possible for you to guarantee a win, given the starting dimensions of the two boards.
NOTE FOR PYTHON USERS: If your program receives TLE (time limit exceeded), you should try submitting using the PyPy interpreter: when you are submitting your code, try using "PyPy 3" or "PyPy 2" as the language, instead of "Python 3" or "Python 2".
Input Specification
The input will be one line, containing four space-separated integers:
Output Specification
Output the character W if you can force a win, or L if your opponent Tyler can force a win.
Constraints and Partial Marks
For
For another
For another
For the remaining
Sample Input 1
2 2 1 3Sample Output 1
WExplanation for Sample Output 1
The sample input indicates that you start with a
On your first turn, if you ignore the
It is easy to see that no matter how Tyler plays his move, he will leave you with at least one
Since you are able to force a win, the output is W.
Sample Input 2
2 2 1 1Sample Output 2
LExplanation for Sample Output 2
Similar to the example above, if you start with a
Since you cannot force a win (instead, Tyler can force you to lose), the output is L.
Comments