Wesley's Anger Contest Reject 1 - Stupendous Bowties 2
View as PDFA Fantastic Right Triangle is a subgraph which uses distinct vertices and
distinct edges, such that each pair of vertices has exactly
edge connecting them.
A Stupendous Bowtie consists of an unordered pair of Fantastic Right Triangles which share exactly one vertex. Count the number of Stupendous Bowties in the given graph with vertices and
edges.
Below is an example of a Stupendous Bowtie:
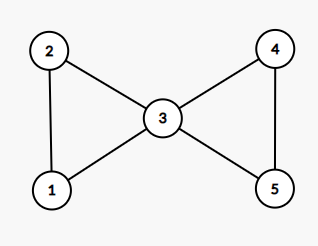
Constraints
For this problem, you will be required to pass all the samples in order to receive points.
and each pair of distinct vertices are connected by at most one edge.
Input Specification
The first line contains two space-separated integers and
.
lines follow; the
one contains two space-separated integers
indicating that vertices
and
are connected by an edge.
Output Specification
This problem is graded with an identical checker. This includes whitespace characters. Ensure that every line of output is terminated with a \n character and that there are no trailing spaces.
Output the number of Stupendous Bowties in the given graph on a single line.
Sample Input 1
5 6
1 2
2 3
3 1
3 4
3 5
4 5Sample Output 1
1Sample Input 2
5 10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5Sample Output 2
15
Comments