Waterloo 2023 Winter D - Link-Cut Tree
View as PDF2023 Winter Waterloo Local Contest, Problem D
BaoBao just learned how to use a data structure called link-cut tree to find cycles in a graph and decided
to give it a try. BaoBao is given an undirected graph with vertices and
edges, where the length of
the
-th edge equals
. She needs to find a simple cycle with the smallest length.
A simple cycle is a subgraph of the original graph containing
vertices
and
edges such that for all
there is an edge connecting vertices
and
in the subgraph.
The length of a simple cycle is the total length of the edges in the cycle.
Input Specification
There are multiple test cases. The first line of the input contains an integer indicating the number of
test cases. For each test case:
The first line contains two integers and
indicating the number of vertices
and edges in the original graph.
For the following lines, the
-th line contains two integers
and
indicating an edge
connecting vertices
and
with length
. There are no self loops nor multiple edges. Note that the
graph is not necessarily connected.
It's guaranteed that neither the sum of nor the sum of
of all test cases will exceed
.
Output Specification
For each test case output one line. If there are no simple cycles in the graph output -1;
Otherwise output integers separated by a space in increasing order indicating the indices of the edges
in the simple cycle with the smallest length. It can be shown that there is at most one answer.
Please, DO NOT output extra spaces at the end of each line, or your answer may be considered incorrect!
Sample Input
2
6 8
1 2
2 3
5 6
3 4
2 5
5 4
5 1
4 2
4 2
1 2
4 3Sample Output
2 4 5 6
-1Explanation for Sample
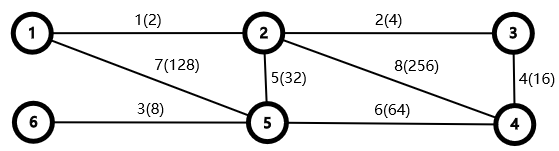
The first sample test case is shown below. The integers beside the edges are their indices (outside the
parentheses) and lengths (inside the parentheses). The simple cycle with the smallest length consists of
edges ,
,
and
with a length of
.
Comments