Woburn Challenge 2018-19 Round 1 - Junior Division

H.S. High School has ~N~ ~(2 \le N \le 100)~ classrooms in a row, numbered from 1 to ~N~ in order. There's a common hallway outside the classrooms with a door to each one, meaning that it's possible to move from the hallway to any classroom (or vice versa) by passing through a door. There's also a door between each pair of adjacent classrooms ~i~ and ~i+1~ (for each ~1 \le i \le N-1~), meaning that it's possible to move between them in either direction by passing through that door.

For example, if ~N = 4~, the school layout looks as follows (with the 4 numbered classrooms at the top, the hallway at the bottom, and doors indicated in brown):

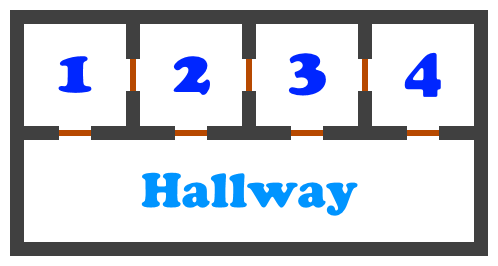
Today, Bob has ~M~ ~(1 \le M \le 100)~ classes to attend, one after another, with the ~i~-th one held in classroom ~C_i~ ~(1 \le C_i \le N)~. Multiple classes throughout the day may be held in the same classroom, but no pair of consecutive classes are held in the same classroom as one another (in other words, ~C_i \ne C_{i+1}~ for each ~1 \le i \le M-1~).

Upon entering the school in the morning, Bob finds himself in the hallway, and will then need to move into his ~M~ classes' classrooms in order (in other words, he'll need to visit classroom ~C_1~, then classroom ~C_2~, and so on). He may freely visit other classrooms or the hallway in between the classes he needs to attend. After attending the ~M~-th class, Bob will need to move back into the hallway before heading home.

Bob is well aware of the alarming volume of germs present on school doorknobs, so he'd like to pass through as few doors as possible throughout the day. Help Bob determine the minimum number of doors he must pass through in total.

Input Specification

The first line of input consists of two space-separated integers, ~N~ and ~M~.
~M~ lines follow, the ~i~-th of which consists of a single integer, ~C_i~, for ~i = 1 \dots M~.

Output Specification

Output a single integer, the minimum number of doors which Bob must pass through in total.

Sample Input

4 5
2
3
1
4
3

Sample Output

8

Sample Explanation

One optimal route Bob might take is as follows:

Hallway ~\to~ Classroom 2 ~\to~ Classroom 3 ~\to~ Classroom 2 ~\to~ Classroom 1 ~\to~ Hallway ~\to~ Classroom 4 ~\to~ Classroom 3 ~\to~ Hallway