Baltic Olympiad in Informatics: 2007 Day 2, Problem 2

Consider a regular grid of ~3N~ points. Every point in the grid has up to eight neighboring points (see Fig. 1). We are interested in counting the number of different ways to connect the points of the grid to form a polygon that fulfills the following conditions:

1. The set of vertices of the polygon consists of all ~3N~ points.

2. Adjacent vertices of the polygon are neighboring points in the grid.

3. Each polygon is simple, i.e. there must not be any self-intersections.

Two possible polygons for ~N = 6~ are given in Figure 2.

Write a program that calculates for a given ~N~ the number of possible ways to connect the points as described modulo ~10^9~.

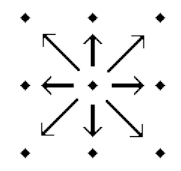
Figure 1: Neighboring points (marked by arrows).

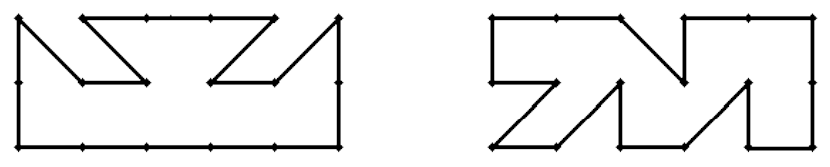
Figure 2: Two possible connections of points for ~N = 6~.

Constraints

~1 \le N \le 10^9~

Subtask 1 [40%]

~1 \le N \le 200~

Subtask 2 [40%]

~1 \le N \le 10^5~

Subtask 3 [20%]

No additional constraints.

Input Specification

The first and only line contains one positive integer ~N~.

Output Specification

Output the number of ways to connect the points modulo ~10^9~.

Sample Input 1

3

Sample Output 1

8

Sample Input 2

4

Sample Output 2

40