COCI '21 Contest 2 #3 Hiperkocka
View as PDFFive in the morning. Daniel wakes up, he opens his eyes. His head hurts a bit. He can still hear the ringing in his ears.
He comes to realize that he has found himself at a playground, in a big metal box.
He remembers a similar situation he found himself in, three years ago, COCI round 2, task Kocka.
But this time, things are much more complicated... Daniel is in an -dimensional hypercube
.
identical copies of a tree
with
edges are scattered around him. It soon became clear to him that salvation lies in tiling the edges of the hypercube with the trees.
Formally, a hypercube is a graph with nodes
, in which nodes
and
are connected if and only if their bitwise xor is a power of two.
A tree can be placed on the hypercube so that:
- each node of the tree corresponds to some node of the hypercube
- those nodes have to be distinct
- if there is an edge between two nodes in the tree, then there has to be an edge between the corresponding nodes in the hypercube.
A tiling of the hypercube is done by placing several trees so that each edge of the hypercube belongs to at most one tree.
Your task is to tile the hypercube with as many copies of the given tree
, which has
edges.
Input Specification
The first line contains a positive integer
, the dimension of the hypercube.
Each of the following lines contains two integers
and
which denote that the nodes
and
are connected by an edge in tree
.
Output Specification
In the first line print the number of trees in your tiling.
Each of the following lines should describe a placement of a single copy of the tree .
In the line print
numbers
. These numbers denote that the
tree is placed so that the hypercube node
corresponds to the tree node
, for all
.
Scoring
If your solution correctly places trees, you will receive
points for that test case, where
Of course, if your solution is not correct, you will receive points.
Your total number of points is equal to the minimum number of points your solution receives over all of the test cases.
It is possible to prove that there always exists a solution which uses all of the trees.
Sample Input 1
1
0 1Sample Output 1
1
0 1Sample Input 2
2
0 1
1 2Sample Output 2
2
0 1 3
0 2 3Sample Input 3
3
0 1
0 2
0 3Sample Output 3
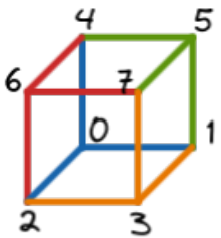
4
0 1 2 4
3 1 2 7
5 1 4 7
6 2 4 7Explanation for Sample Output 3
Comments