You are given a tetromino ~T~, (O, I, T, J, L, S, or Z), and an infinite grid of integers extending in all four directions. Every integer in the grid is initially equal to ~0~. However, Marcus will perform a series of ~Q~ updates to the grid, where the ~i^{th}~ update adds ~v_i~ to the integer at the coordinates ~(x_i, y_i)~.

After each update, Marcus wants you to solve the following problem:

You may translate and rotate (but not reflect) your given tetromino ~T~ anywhere on the grid such that it covers exactly four integers. In one operation, you can add any integer ~k~ to all four integers currently covered by the tetromino. It is permitted for ~k~ to be negative.

Can you determine if it is possible to make all of the integers in the infinite grid equal to ~0~ in a finite number of operations? If so, output YES. Otherwise, output NO.

Note: The positive ~x~ direction is right, and the positive ~y~ direction is up.

Constraints

~T \in \{~O~,~I~,~T~,~J~,~L~,~S~,~Z~\}~

~1 \le Q \le 10^6~

~1 \le x_i, y_i, \le 10^6~
~1 \le |v_i| \le 10^6~

~T~	Shape	Marks
O		20/100
I		20/100
T		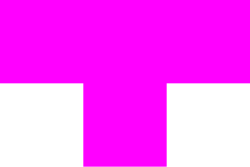20/100
J		10/100
L		10/100
S		10/100
Z		10/100

Input Specification

The first line contains one character, ~T~, the given tetromino.

The next line contains one integer, ~Q~, the number of updates.

The next ~Q~ lines each contain three space-separated integers, ~x_i~, ~y_i~, and ~v_i~, indicating that ~v_i~ is added to the integer at ~(x_i, y_i)~.

Output Specification

Output ~Q~ lines, the ~i^{th}~ line containing YES if it is possible to make all of the integers in the infinite grid equal to ~0~ after the first ~i~ updates, and NO, otherwise.

Sample Input 1

O
9
3 3 1
3 4 1
4 4 1
4 3 2
4 3 -1
2 2 -3
2 5 -3
5 5 -3
5 2 -3

Sample Output 1

NO
NO
NO
NO
YES
NO
NO
NO
YES

Explanation for Sample 1

The first update, 0 0 1, adds ~1~ to the integer at ~(0,0)~. It can be shown that it is impossible to make all integers in the grid equal to ~0~ in this state. Thus, the correct output is NO. This will be true up until the fifth update, where the grid looks like this (~0~'s in unmodified cells are omitted for better viewing):

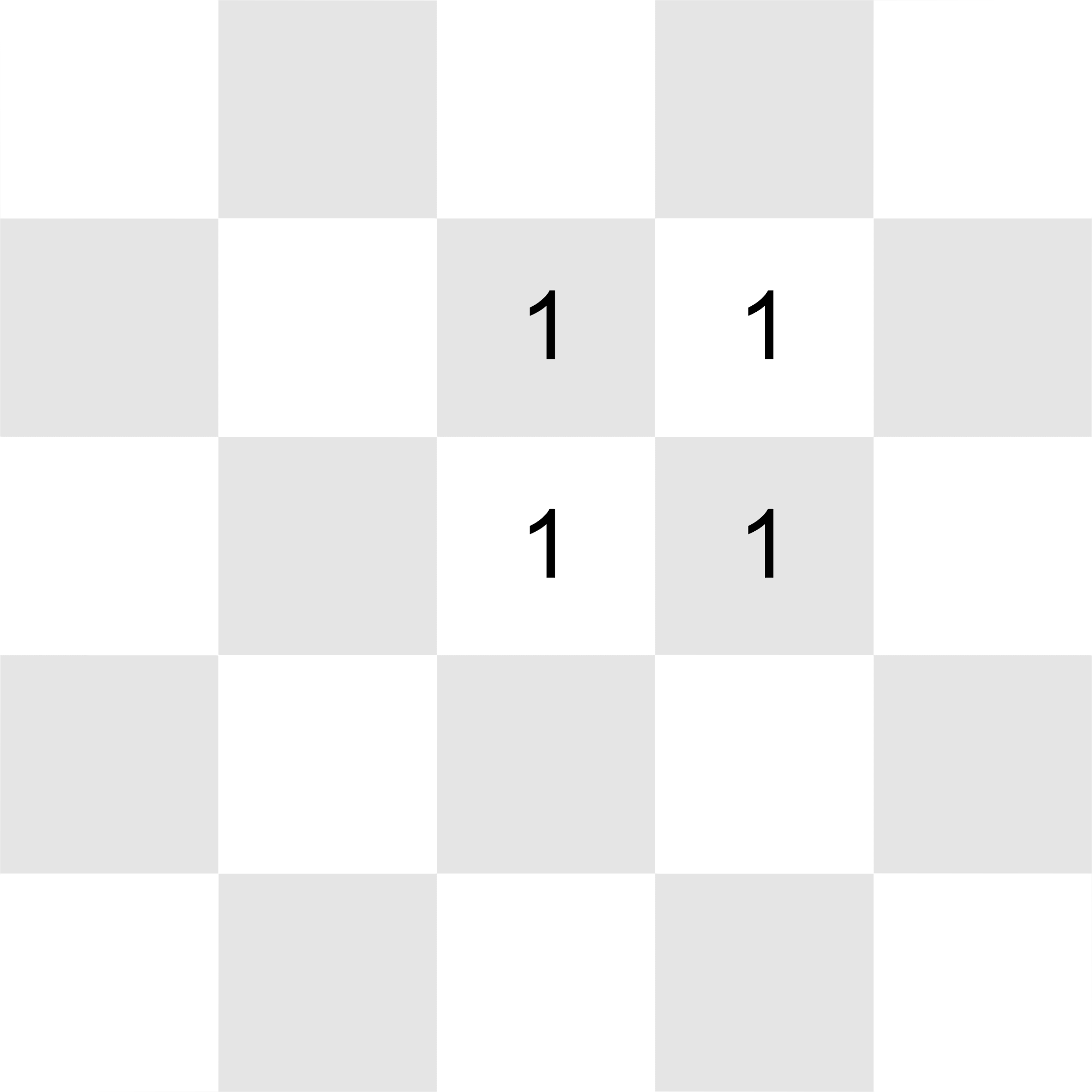
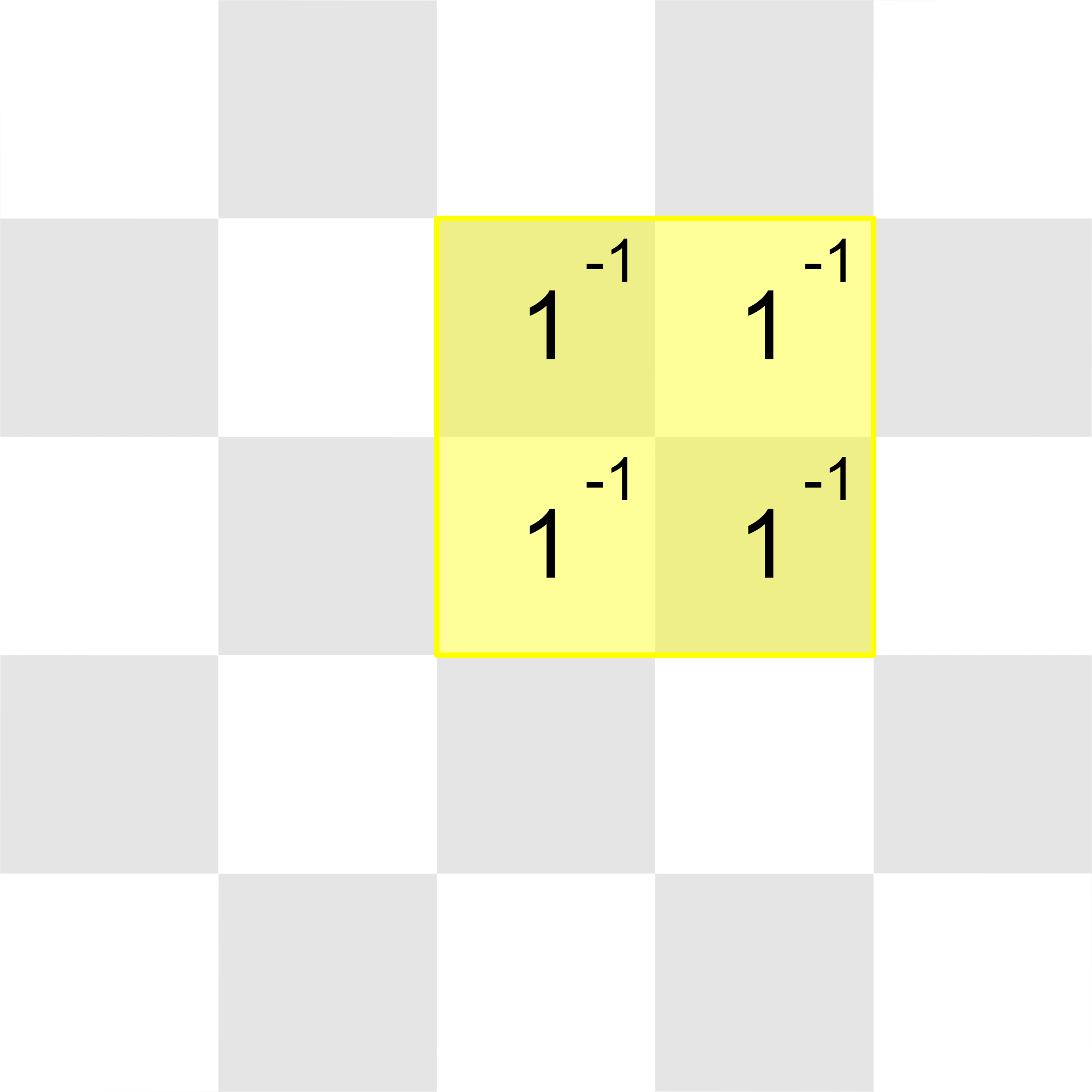
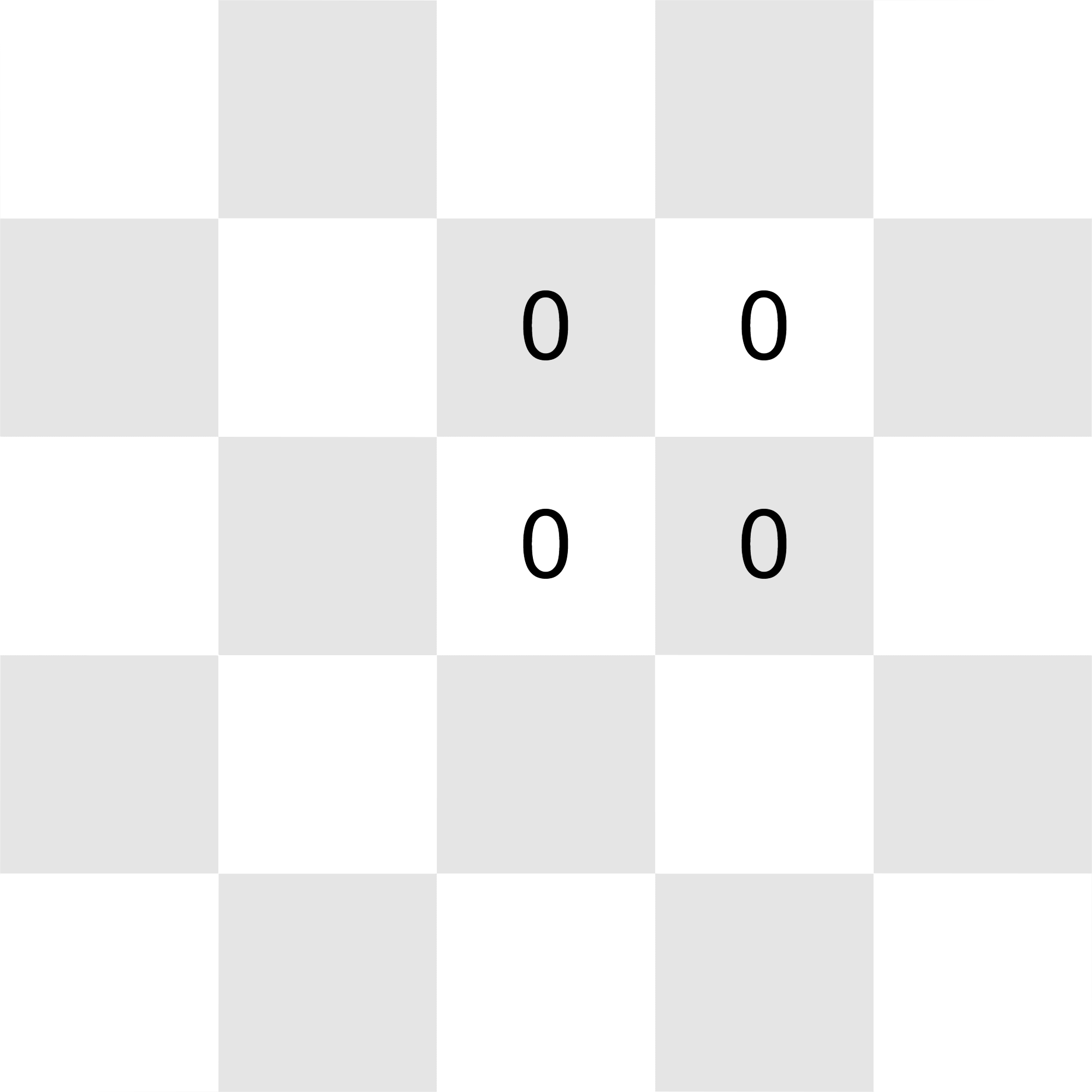
All of the integers in the grid can be reduced to ~0~ by placing the O tetromino on top of the four ~1~'s, and subtracting ~1~ from each of them.

Thus, the correct output after the fifth update is YES.

The next update, -1 -1 -3, adds ~-3~ to the integer at ~(-1,-1)~. It can be shown that it is impossible to make all integers in the grid equal to ~0~ in this state. Thus, the correct output is NO.

After all the updates, the grid will look like this (once again, ~0~'s in unmodified cells are omitted for better viewing):

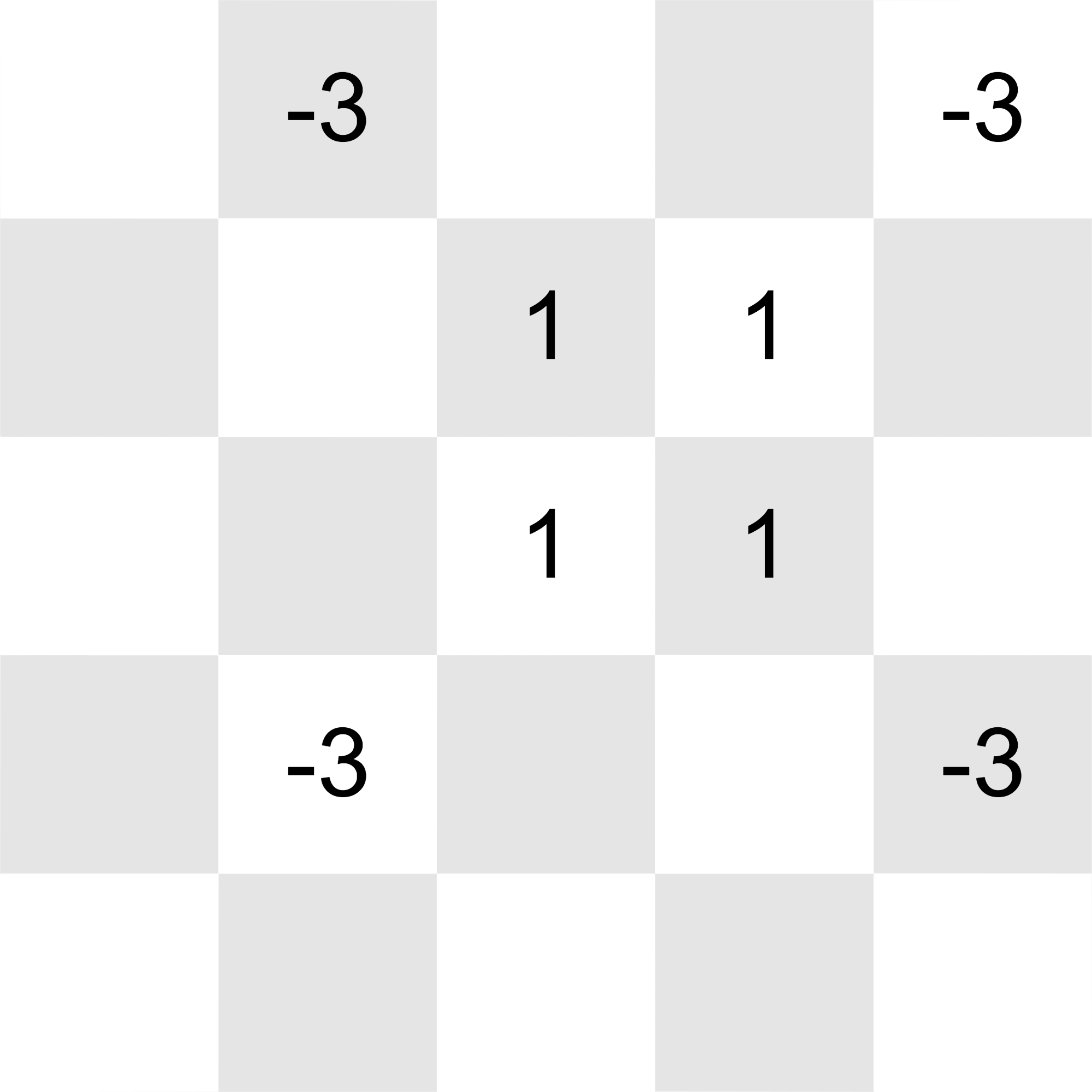
All of the integers in the grid can be reduced to ~0~ with these operations:

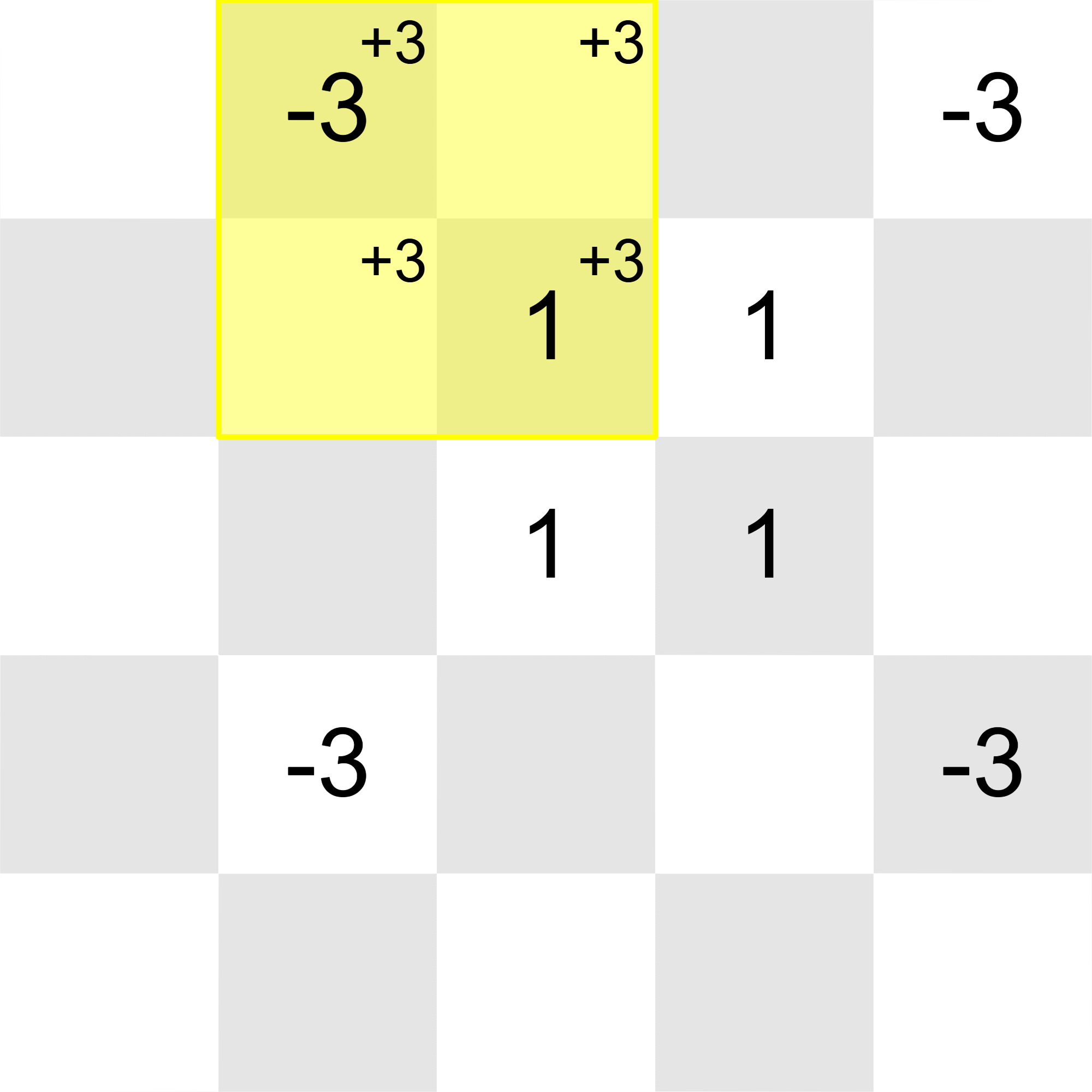
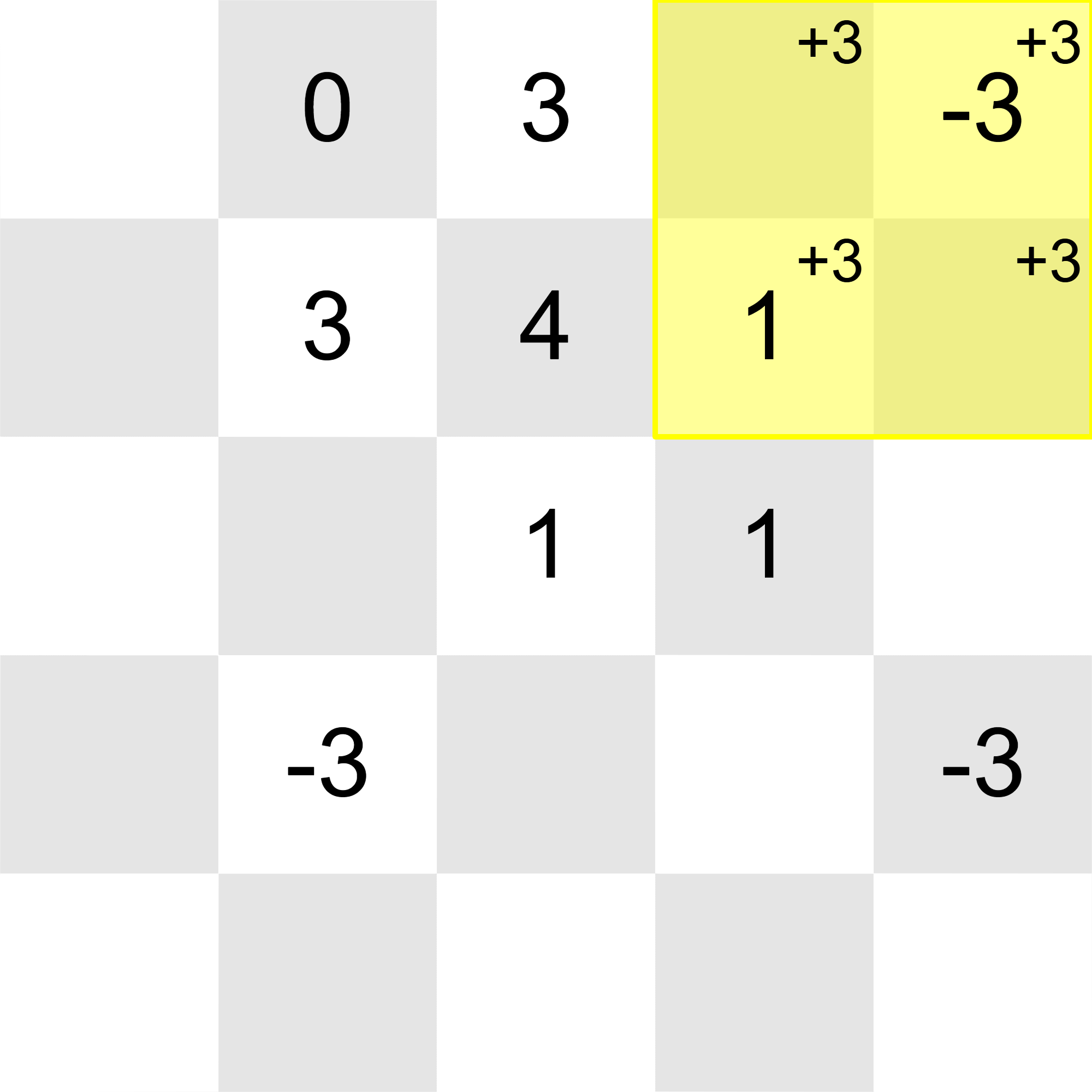
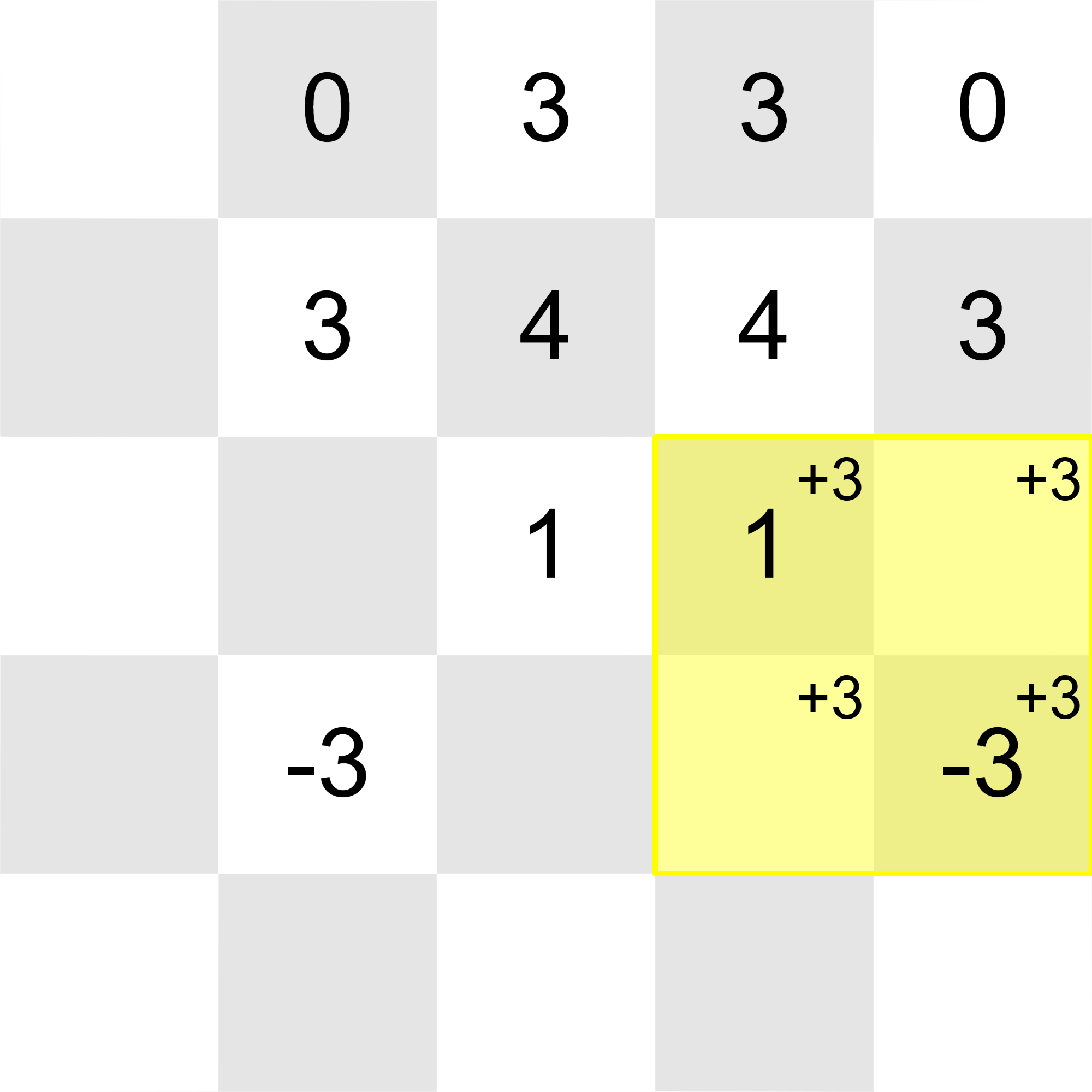
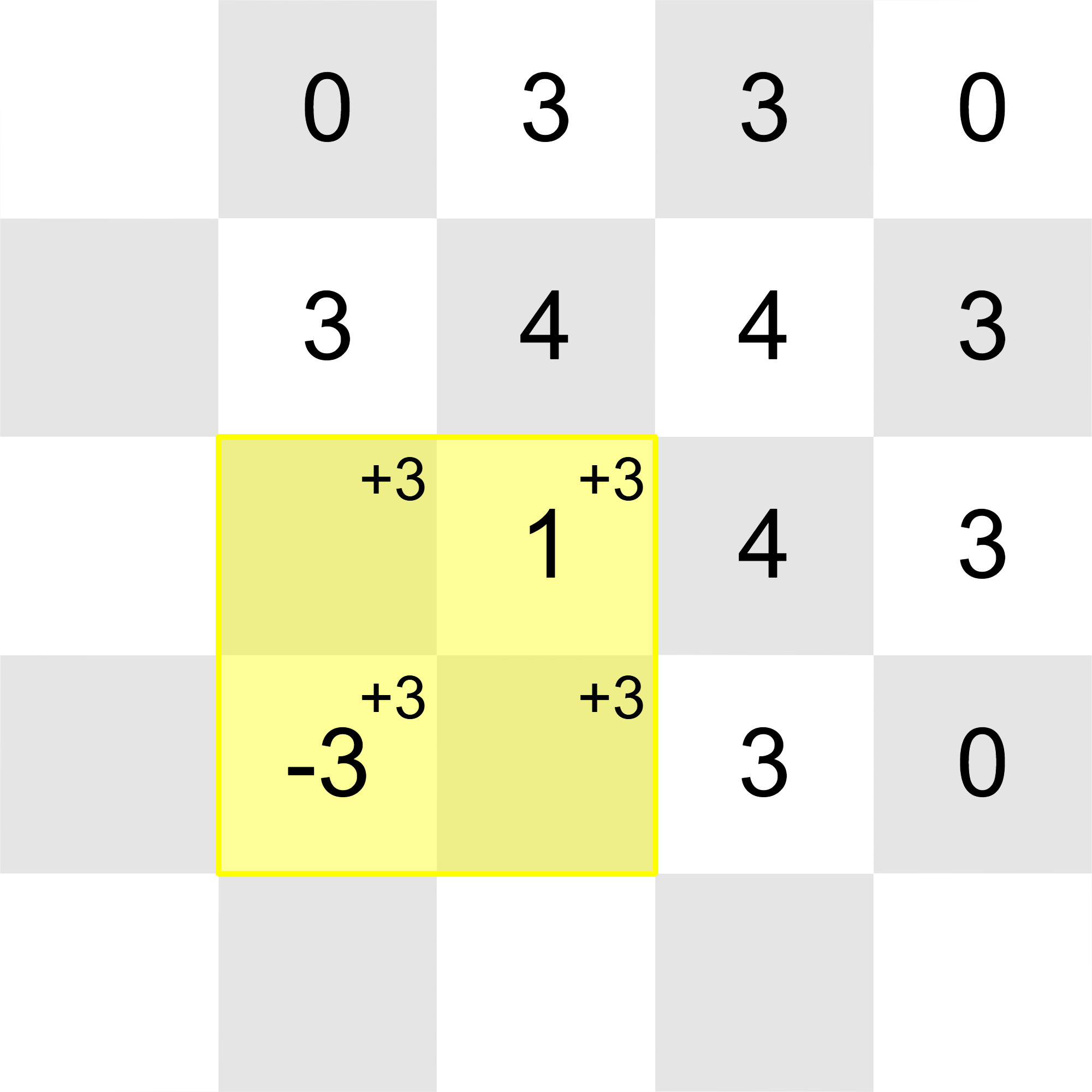
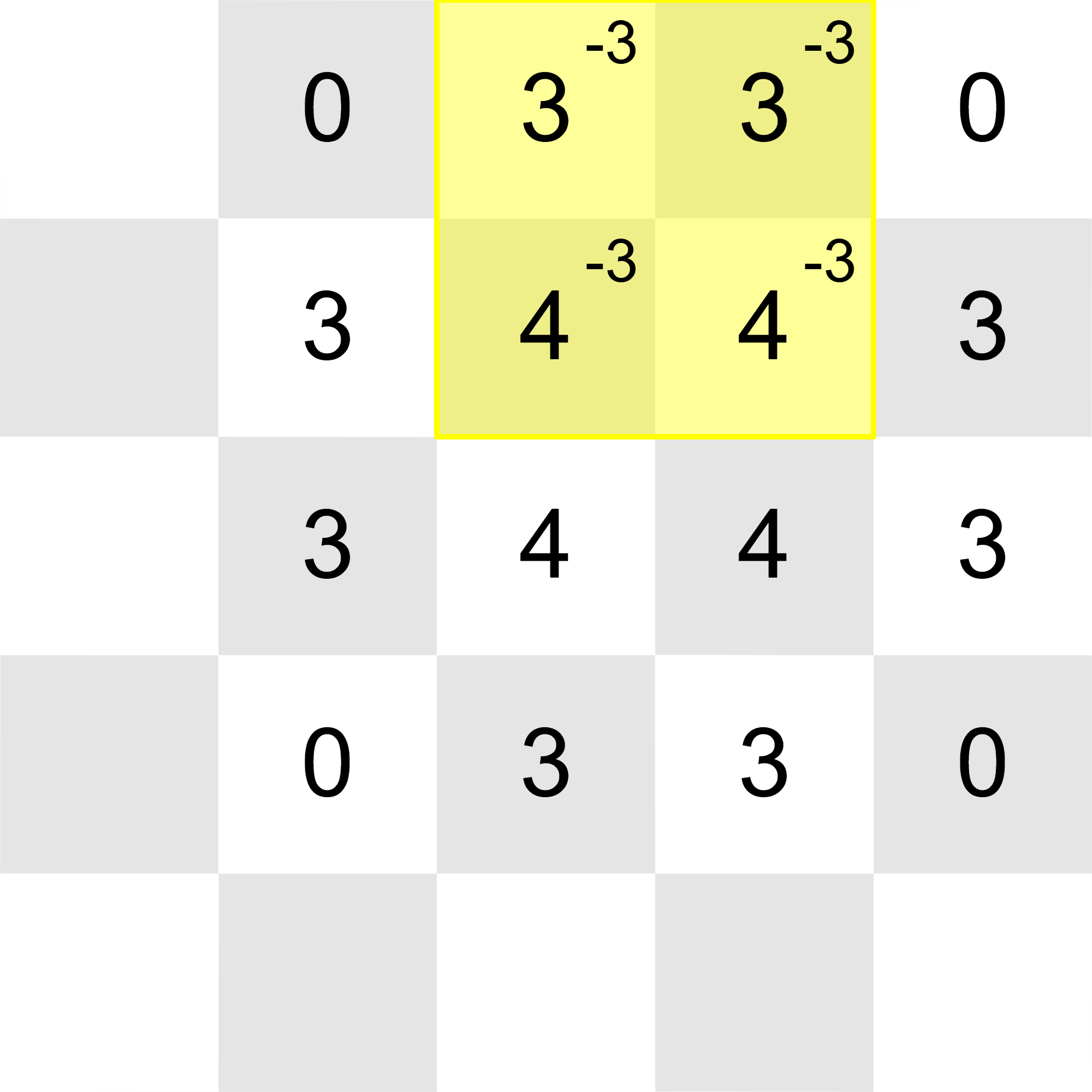
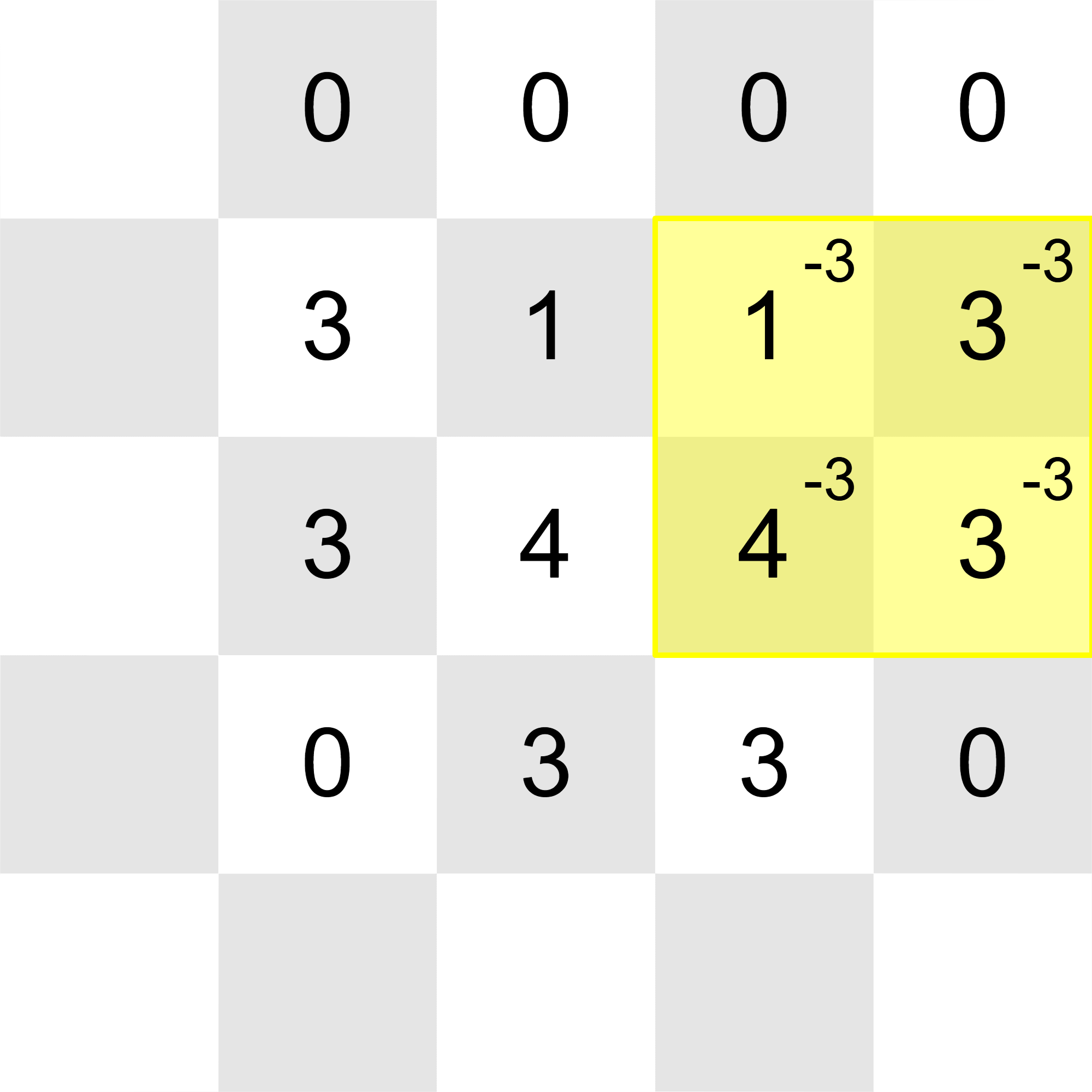
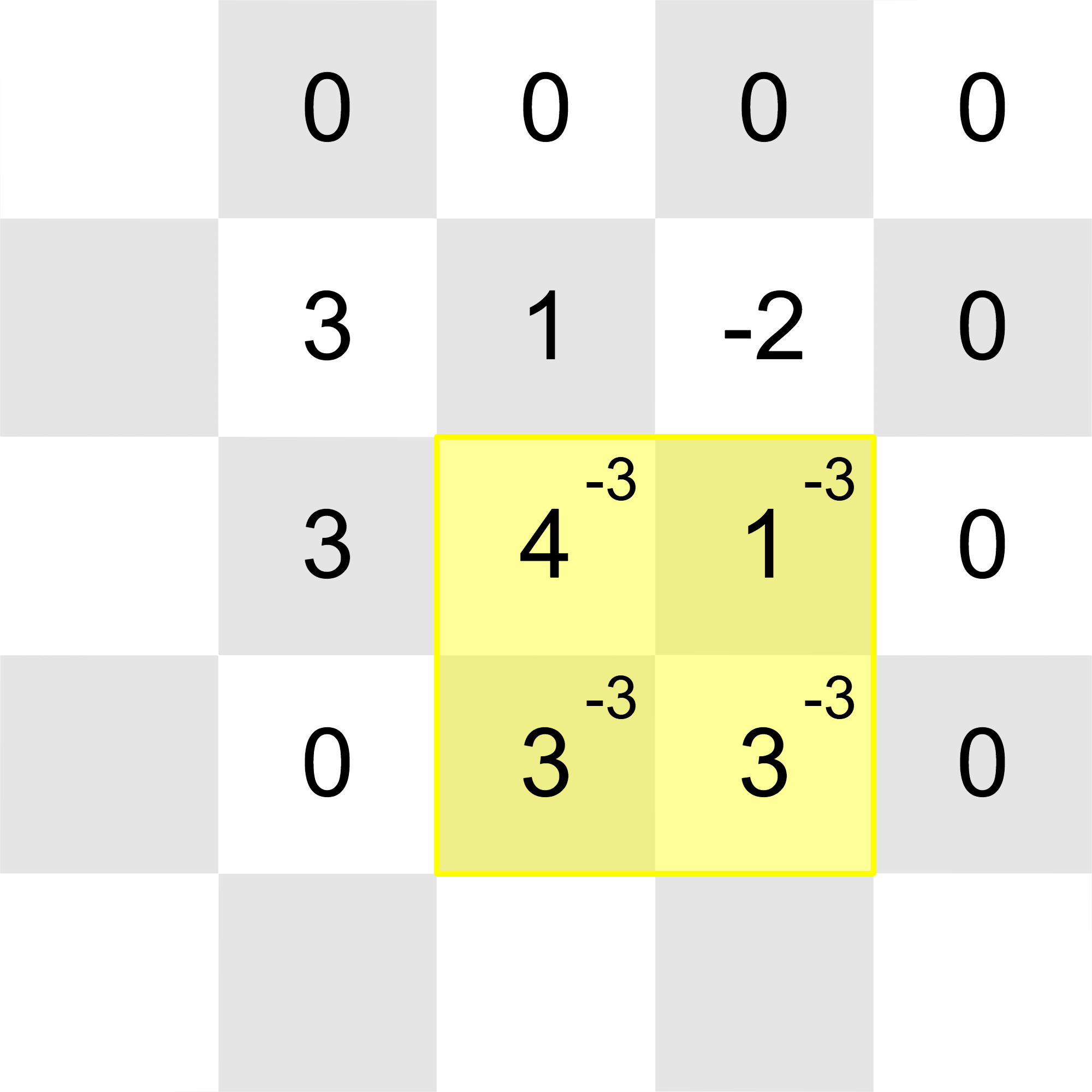
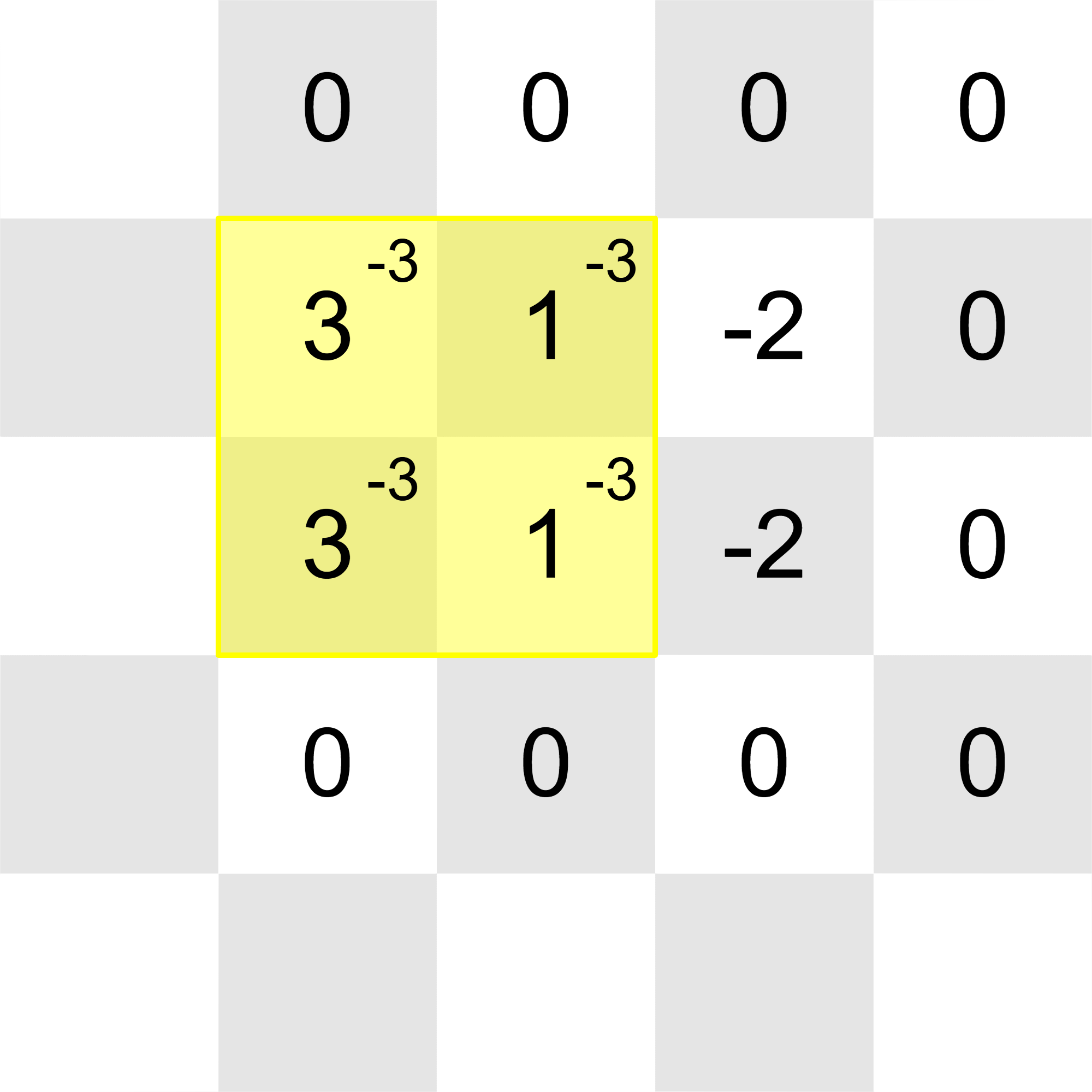
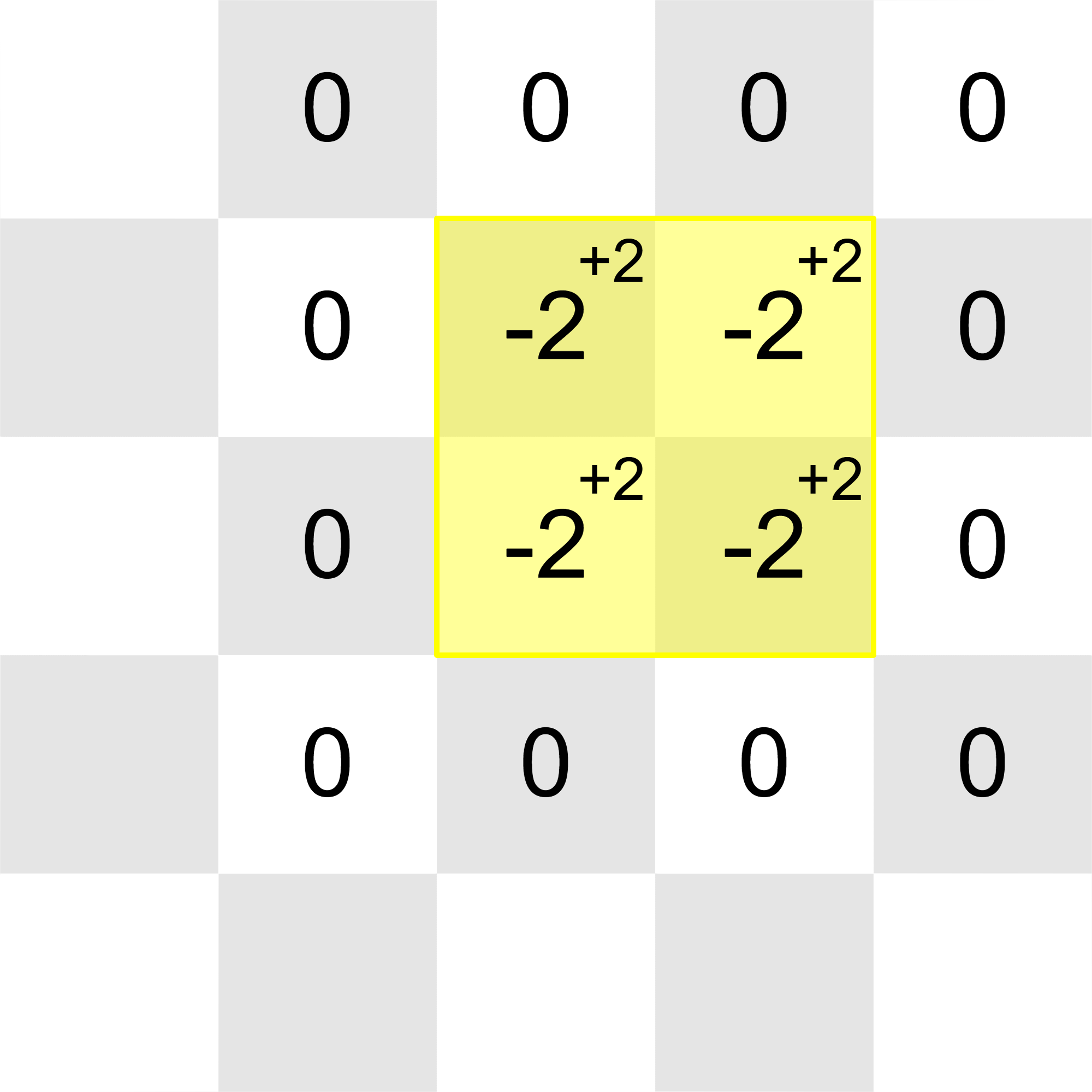
Thus, the correct output after the final update is YES.

Sample Input 2

T
10
2 2 10
1 1 1
2 1 -4
1 2 6
3 3 8
3 1 -1
1 3 11
2 3 5
3 2 3
1 1 1

Sample Output 2

NO
NO
NO
NO
NO
NO
NO
YES
NO
YES

Explanation For Sample 2

After all the updates, the grid will look this:

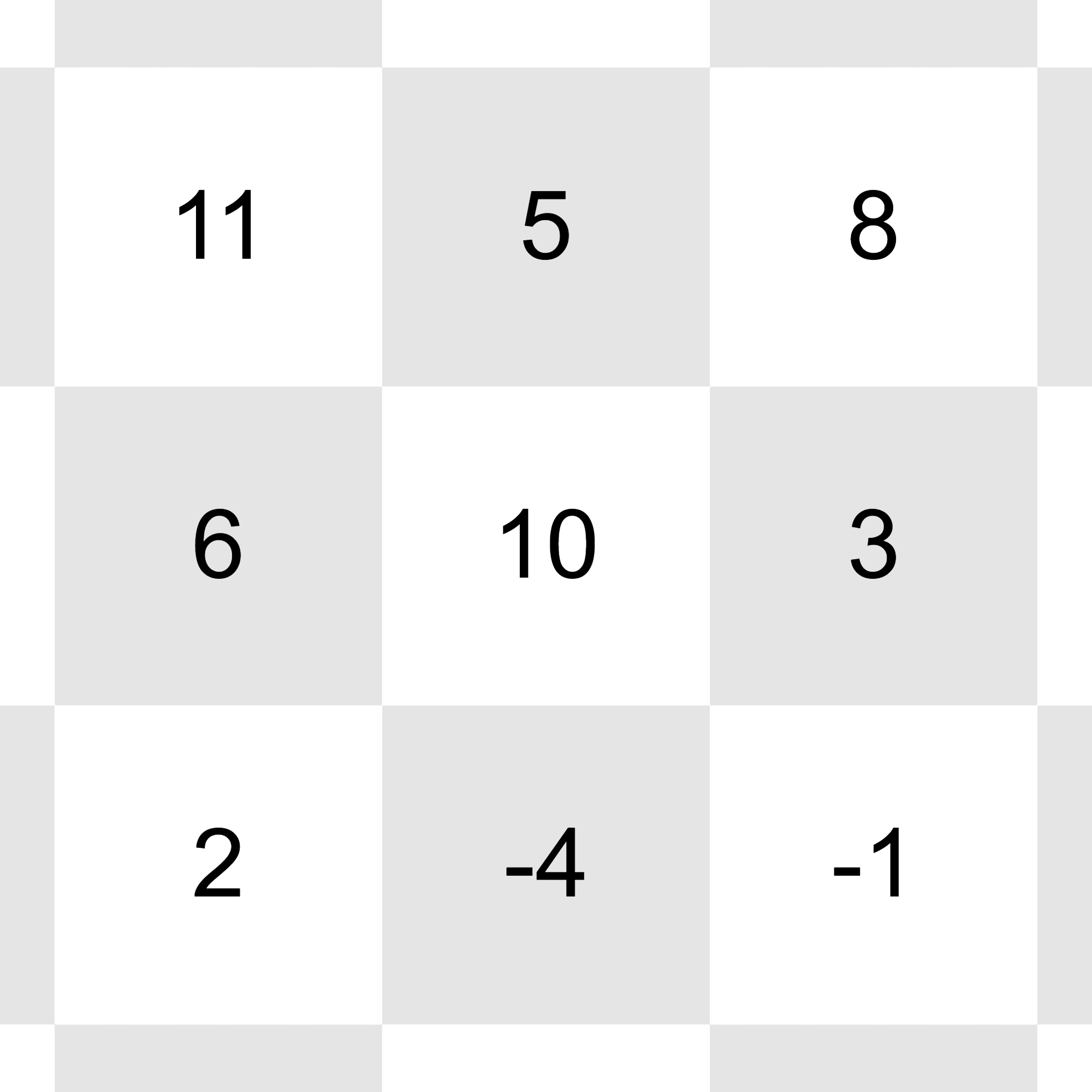
All of the integers in the grid can be reduced to ~0~ with these operations:

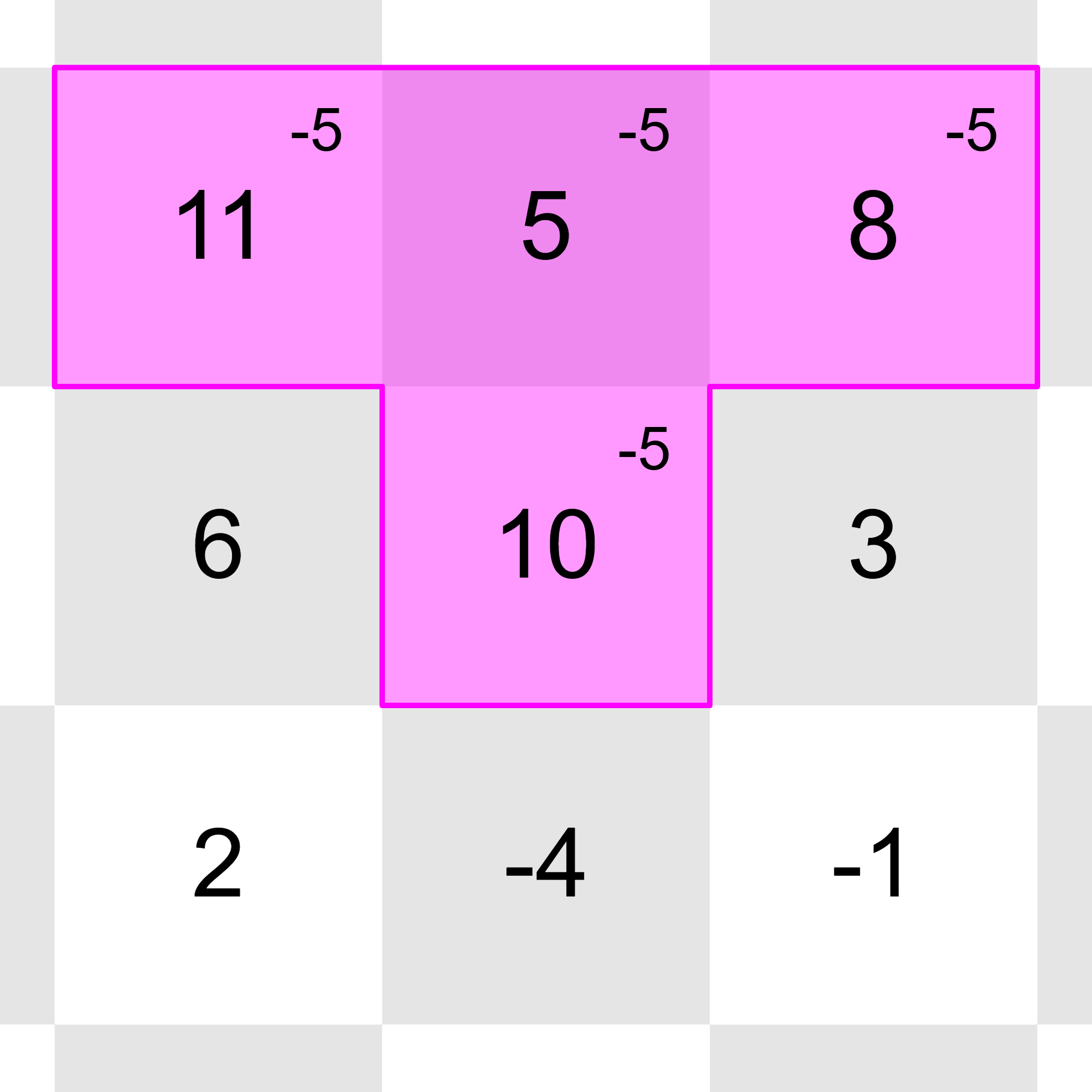
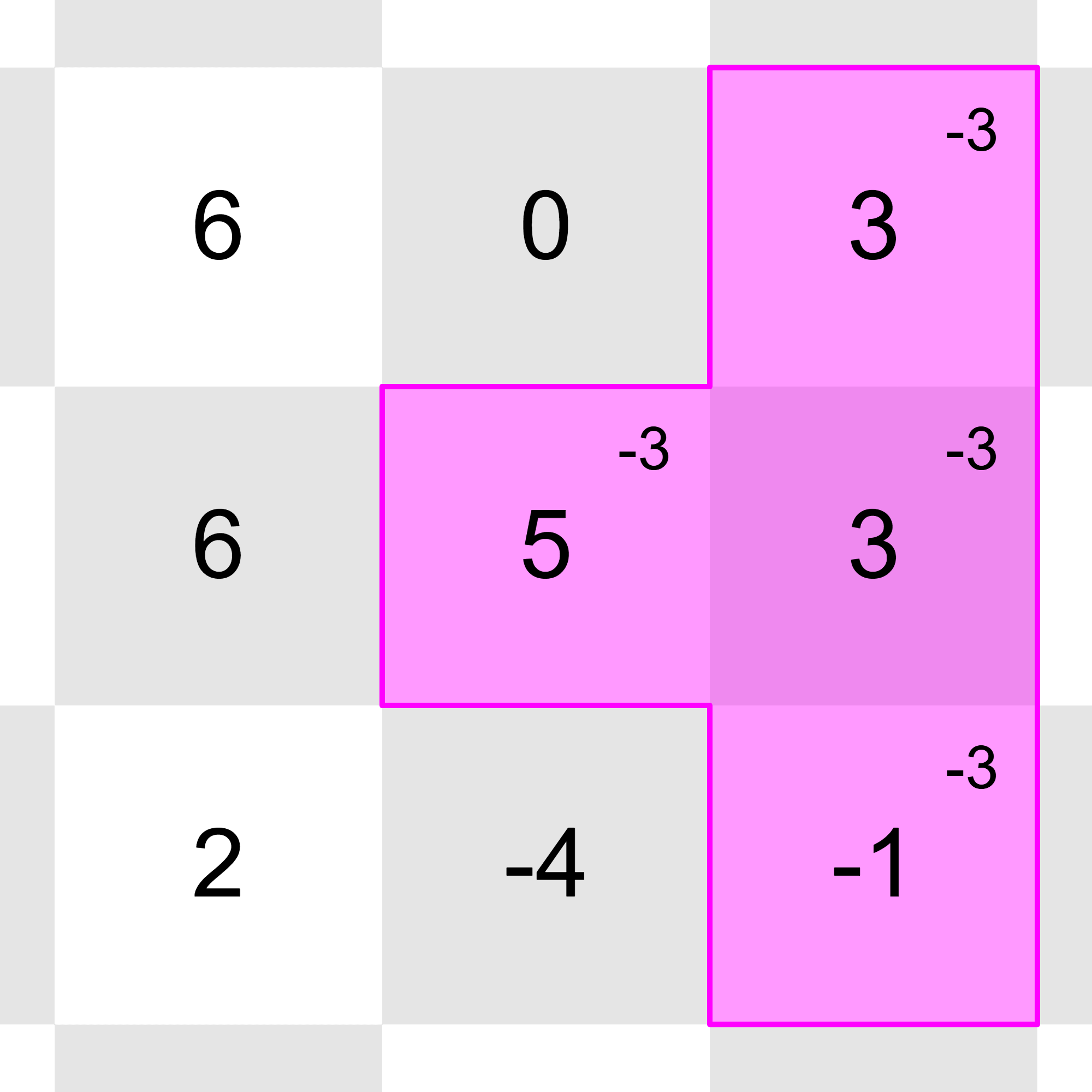
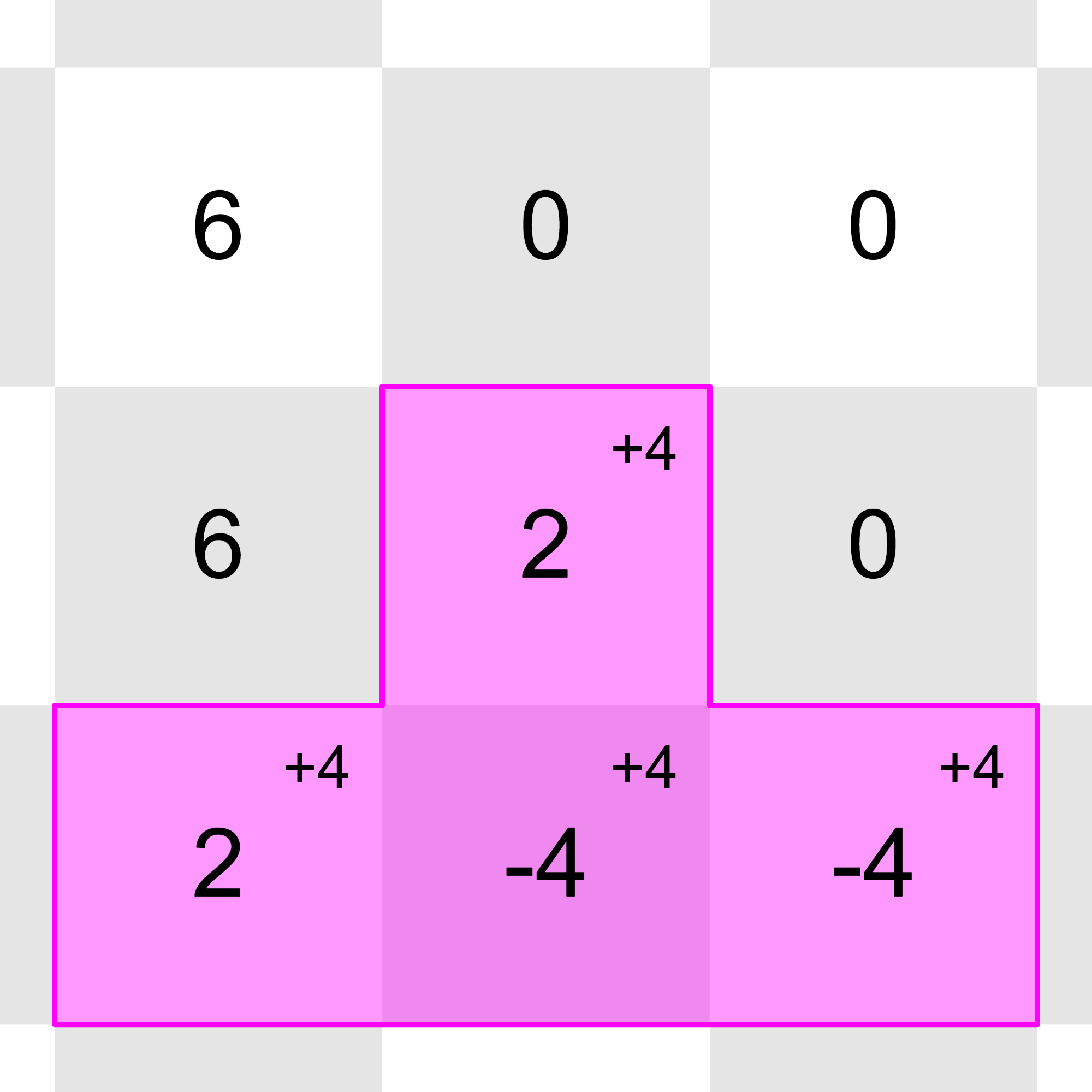
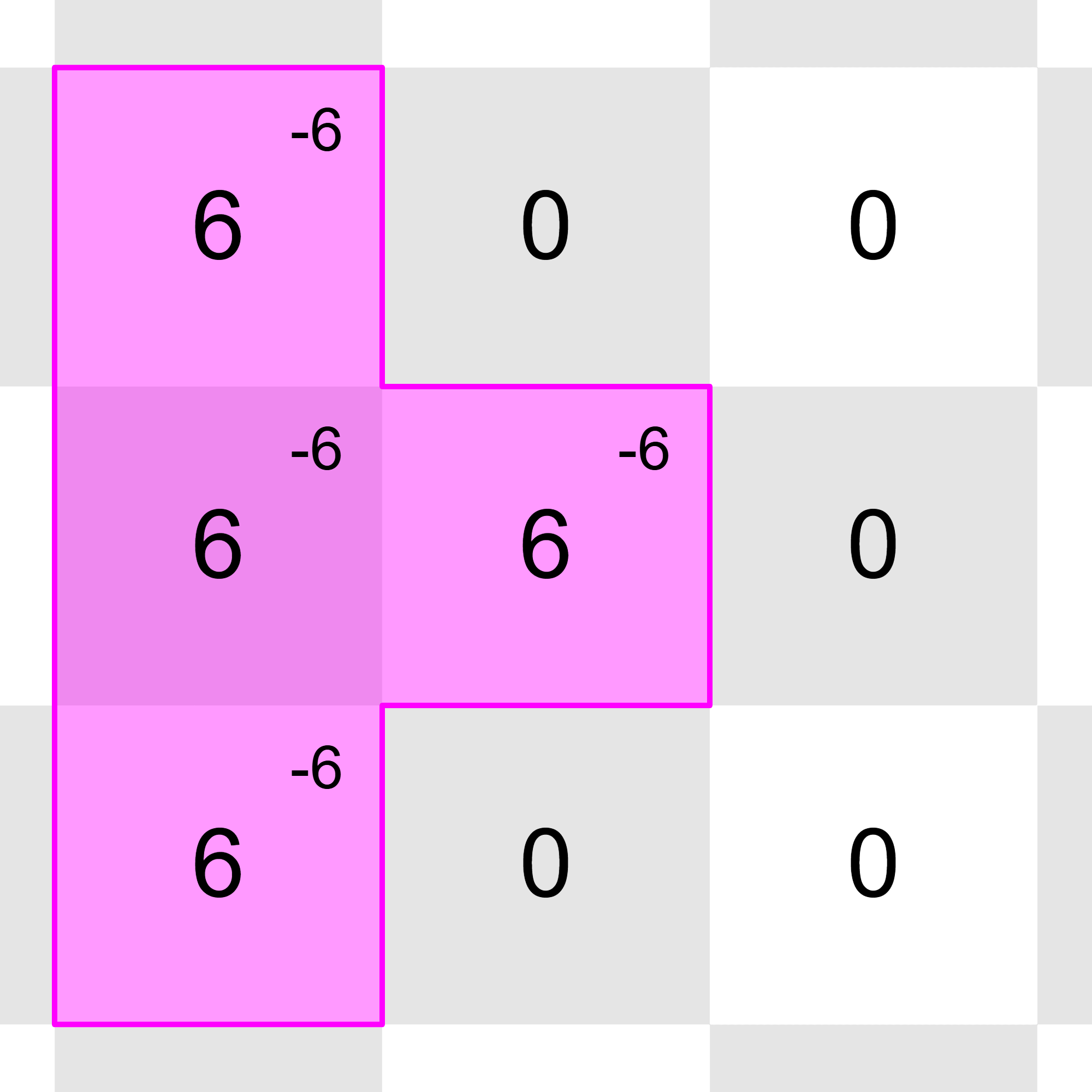
Sample Input 3

Z
8
1 1 1
2 1 1
2 2 1
3 2 1
1 1 -1
3 2 -1
1 2 1
3 1 1

Sample Output 3

NO
NO
NO
NO
NO
NO
NO
YES

Explanation for Sample 3

Remember that translations and rotations are allowed, but reflections are not.