Editorial for IOI '14 P5 - Friend
Submitting an official solution before solving the problem yourself is a bannable offence.
Subtask 1
In subtask 1, is at most
. So just apply backtracking for every person – to choose or not to choose. The complexity is
.
The sizes of in other subtasks are too large to apply this solution, resulting in Time Limit Exceeded with this complexity.
Subtask 2
In subtask 2, all relations are MyFriendsAreYourFriends, forming a graph with no edge. That is equivalent to choosing all persons, with a complexity of .
Subtask 3
In subtask 3, all relations are WeAreYourFriends, forming a complete graph. Since every pair of two persons is connected by an edge, the answer to this problem is equivalent to choosing the maximum confidence among all people, with a complexity of .
Subtask 4
In subtask 4, all relations are IamYourFriend, forming a tree. So we apply the DP-in-tree method.
Define as the maximum sum for the
node with status
, where
stands for not choosing this node and
stands for choosing this node. Then:
If the
node is leaf, then
, for
.
, for
.
Otherwise,
, for
and for all
, where
is
's child.
, for
and for all
, where
is
's child.
The final answer is , where
stands for the root of this tree.
Subtask 5
Since there are only MyFriendsAreYourFriends and IamYourFriend relations, the resulting graph contains no odd cycle. That is, we obtain a bipartite graph. With all confidence equals to , the problem becomes finding maximum independent set in a bipartite graph. As we know, a set is independent if and only if its complement is a vertex cover. If the complement of independent set is not a vertex cover, then there exists at least one edge with end points
and
, which is included in the independent set, conflicting with the definition of independent set. Trivially, a maximum independent set is the complement of minimum vertex cover.
According to Kőnig's theorem, in any bipartite graph, the number of edges in a maximum matching is equal to the number of vertices in a minimum vertex cover. Thus, we can apply the augmenting path algorithm to find out maximum cardinality matching in a bipartite graph, with complexity of or
, depending on different implementations, where
is the number of edges.
Let be the result of maximum cardinality bipartite matching, the answer to this problem equals
, since maximum independent set is the complement of minimum vertex cover.
As for partitioning the graph into bipartite, we apply dfs to mark out the odd points and the even points, and then put all odd points on one side, even points on the other side.
In subtasks 2 and 4, the relations are MyFriendsAreYourFriends and IamYourFriend. However, the confidence values in those two subtasks are not all equal to . As a result, this solution can only solve subtask 5 correctly, and Wrong Answer for other subtasks.
Subtask 6
By using Greedy method to eliminate each person in the reverse order of building process, we will finally get the pair for the last person. The answer will be
of the last person.
Here, we briefly introduce this method. Initially, we maintain two values and
for each person
, where
and
. Physically,
stands for 'choose' and
stands for 'not choose'.
To simplify the notation, we call for
,
for
,
for
,
for
.
WeAreYourFriends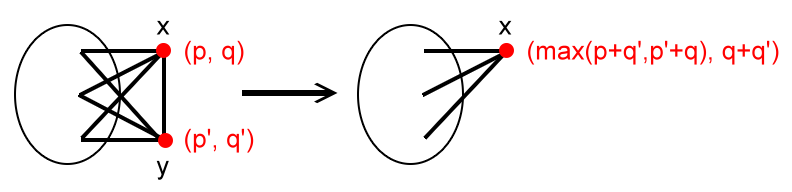
To eliminate, we can choose
, or choose
, or choose neither.
- Choose
:
.
- Choose
:
.
- Neither:
. So
,
.
- Choose
MyFriendsAreYourFriends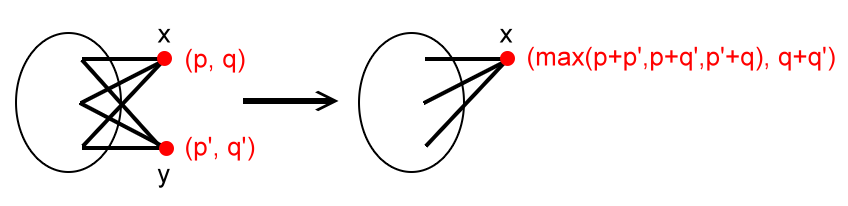
To eliminate, we can choose
, or choose
, or choose both, or choose neither.
- Choose
:
.
- Choose
:
.
- Choose both:
.
- Neither:
. So
,
.
- Choose
IamYourFriend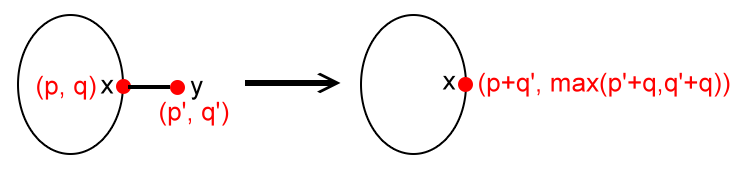
To eliminate, we can choose
, or choose
, or choose neither.
- Choose
:
.
- Choose
:
.
- Neither:
. So
,
.
- Choose
The complexity of this scheme is . This method is capable of solving all subtasks.
Comments