IOI '96 - Veszprém, Hungary

A factory is running a production line. Two operations have to be performed on each job: first operation A, then operation B. There is a certain number of machines capable of performing each operation.

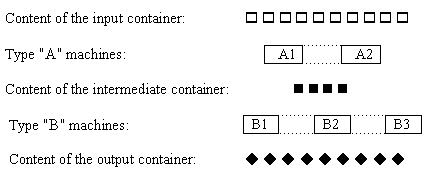
The figure above shows the organisation of the production line that works as follows. A type A machine takes a job from the input container, performs operation A and puts the job into the intermediate container. A type B machine takes a job from the intermediate container, performs operation B and puts the job into the output container. All machines can work in parallel and independently of each other, and the size of each container is unlimited. The machines have different performance characteristics, a given machine works with a given processing time.

Give the earliest time operation A can be completed for all ~N~ jobs provided that the jobs are available at time ~0~. Compute the minimal amount of time that is necessary to perform both operations (successively, of course) on all ~N~ jobs.

Input Specification

• Line 1: One integer ~N~, the number of jobs ~(1 \le N \le 1\,000)~.
• Line 2: One integer ~M_1~ ~(1 \le M_1 \le 30)~, the number of type A machines.
• Line 3: ~M_1~ integers, the job processing times of each type A machine.
• Line 4: One integer ~M_2~ ~(1 \le M_2 \le 30)~, the number of type B machines.
• Line 5: ~M_2~ integers, the job processing times of each type B machine.

The job processing time is measured in units of time, which includes the time needed for taking a job from a container before processing and putting it into a container after processing. Each processing time is at least ~1~ and at most ~20~.

Output Specification

Your program should output two integers on separate lines. The first line should contain the minimum time to perform all A tasks, and the second should contain the minimum time to perform all B tasks (which require A tasks, of course).

Sample Input

5
2
1 1
3
3 1 4

Sample Output

3
5