Frieren is analyzing a magic barrier, whose strength at specific points can be represented as a 2D grid, ~a~, with ~N~ rows, ~M~ columns, and unique values. Specifically, the strength of the barrier on the ~r^{th}~ row and ~c^{th}~ column is ~a_{r,c}~. She asks you ~Q~ questions in the form of ~(k,r_1,c_1,r_2,c_2)~ and your task for each of them is to determine whether ~k~ exists in the inclusive rectangle formed by ~a_{r_1, c_1}~ and ~a_{r_2, c_2}~.

Note: Fast input is highly recommended for this problem. Also, Python users should submit with PyPy as it is significantly faster.

Constraints

All values of ~a_{r,c}~ are unique.

~1 \le k, a_{r,c} \le 10^9~

~1 \le r_1 \leq r_2 \le N~

~1 \le c_1 \leq c_2 \le M~

Subtask 1 [15%]

~1 \le N,M,Q \le 10~

Subtask 2 [85%]

~1 \le N,M \le 1000~

~1 \le Q \le 2 \times 10^5~

Input Specification

The first line contains ~3~ integers, ~N~, ~M~, and ~Q~.

The next ~N~ lines contain ~M~ integers each, representing the barrier strength ~a_{r,c}~.

The next ~Q~ lines contain ~5~ integers each, ~k,r_1,c_1,r_2,c_2~.

Output Specification

For each question, output yes if the ~k~ for that question exists in the given rectangle and no otherwise.

Sample Input 1

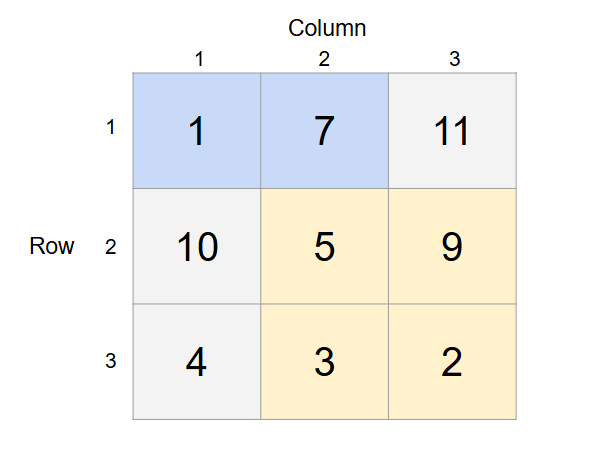
3 3 3
1 7 11
10 5 9
4 3 2
10 1 1 1 2
3 2 2 3 3
100 2 2 3 3

Sample Output 1

no
yes
no

Explanation for Sample Output 1

The rectangle for the first question is shown in blue. ~10~ is not inside it.

The rectangle for the second question is shown in yellow. ~3~ is inside it.

The rectangle for the third question is shown in yellow. ~100~ is not inside it (it's not even in the grid).

Sample Input 2

2 3 2
1 2 3
4 5 6
1 1 1 1 1
1 2 2 2 3

Sample Output 2

yes
no